ЛАБОРАТОРНАЯ РАБОТА №11 ОПРЕДЕЛЕНИЕ КАЧЕСТВЕННЫХ ХАРАКТЕРИСТИК ТОРМОЗНОГО РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ
Цель работы: ознакомиться с расчетом основныххарактеристик тормозного рентгеновского излучения.
Приборы и принадлежности: дентальная рентгеновская установка, рентгенометр ДФТЗ-02, набор поглощающих пластин из алюминия, меди, костной ткани и оргстекла.
Порядок выполнения работы : Произведите измерения экспозиционной дозы, последовательно увеличивая количество пластин, т.е.толщину поглощающего вещества. Последовательность операций следующая: 1) Перед включением рентгеновской установки установить время экспозиции 30 с с помощью реле времени. С помощью дистанционного устройства включите рентгеновскую установку, измерьте экспозиционную дозу Do и запишите в таблицу измерений 2) После того, как реле времени сработало, и рентгеновская установка выключилась, установите на подставке поглощающую пластину. 3) Снова включить рентгеновскую установку и повторить измерение экспозиционной дозы. Толщина поглотителя х определяется суммарной толщиной всех пластин, установленных для данного измерения на подставке. 4) При измерении экспозиционной дозы с алюминиевым фильтром, меняющем спектральный состав тормозного излучения рентгеновской трубки, последний устанавливается сразу на выходе источника рентгеновского излучения.
Данные измерений записаны в таблицу 1. Таблица 1
Обработка результатов измерений : 1.Определите процентные дозы по формуле: 2. На листе миллиметровой бумаги постройте кривые ослабления (зависимость процентных доз от толщины поглотителя). 3. Определите слой половинного ослабления ∆½ и слой 25% ослабления ∆1/4 для каждой серии измерений.Рассчитайте коэффициент однородности излучения по формуле:
4. Рассчитайте эффективный линейный коэффициент для всех рассматриваемых случаев по формуле: Расчёт погрешности определения μэфф
Погрешность определения коэффициента линейного ослабления
5. Произведите расчет массового коэффициента ослабления μ эфф м 6. Определите граничную энергию тормозного излучения Е г. Найдите в таблице 2 эффективную энергию, соответствующую данному значению массового коэффициента ослабления μ эфф м
Таблица 2. Значение массовых коэффициентов ослабления для фотонов различной энергии в ряде поглощающих сред
7.Сделайте вывод: достигнута ли цель работы, какое явление наблюдали, ответьте на следующие вопросы: 1) Какова граничная энергия тормозного излучения для данного режима работы рентгеновской установки? Достаточна ли она для ионизации материала? 2) Сравнить проникающую способность фильтрованного и нефильтрованного излучения по величине слоя половинного ослабления. 3) Как меняется коэффициент однородности излучения с применением фильтра и без него? Оценить величину погрешностей
Дайте теоретическое обоснование работы, опираясь на вопросы для самоподготовки
Вопросы для самоподготовки: 1. Работа рентгеновской трубки. 2. Приборы и методы регистрации ионизирующих излучений. 3. Основные дозиметрические характеристики ионизирующего излучения. 4. Закон ослабления узкого луча моноэнергетического излучения. Слой половинного ослабления. Ослабление немоноэнергетического ионизирующего излучения. Эффективный линейный коэффициент ослабления. Задачи: Ремизов А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике. 3-е изд., –Москва, Дрофа, 2010 №№ 7.58, 7.59,7.61,7.72 Литература: 1.Лекции 2.Ремизов А.Н.Медицинская и биологическая физика. -М. Высшая школа 2003,гл.26,28 3.Карелин А.О., Кулинкин А.Б., Марущак В.А., Мещанинова В.В., Михайлова И.А., Поспелова И.И., Рукавцова О.М., Соколов Д.В. Краткие основы физики ионизирующего излучения, применение его в медицине и нормирование. Издательство СПбГМУ 2001
ЛАБОРАТОРНАЯ РАБОТА № 12 ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ ГАУССА.ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ. Цель работы : В настоящей работе изучается экспериментальное распределение значений непрерывной случайной величины. В качестве значений исследуемой случайной величины могут использоваться значения, моделируемые генератором случайных чисел. Данная модель представляет собой результаты измерений некоторой непрерывной случайной величины, выбранные случайным образом.
Порядок выполнения работы :
1. Результаты измерений занести в таблицу 1, которая составляет статистический ряд. Таблица1.
2. Простой статистический ряд преобразуйте в упорядоченный статистический ряд. Для этого в таблице 1 найдите максимальное и минимальное значения и весь диапазон
Для определения количества интервалов можно воспользоваться правилом Стерджеса:
Верхние границы каждого из k интервалов вычислите по формуле:
Найдите число попавших в интервал значений mj,статистическую вероятность
Вычисленные данные занесите в таблицу 2. Таблица2.
величины по формуле: просуммировав данные седьмого столбца таблицы2.
просуммировав данные восьмого столбца таблицы2.
подставляя вместо a и b верхние и нижние границы интервала. Вычисленные значения занесите в таблицу 3.
Определите значения функции Гаусса(нормальной функции распределения) для соответствующих
Затем по формуле:
найдите теоретическую вероятность попадания случайной величины в заданный интервал и также занесите в таблицу 3. Таблица3.
6. На листе миллиметровой бумаги постройте экспериментальные Pj и теоретические P теор распределения вероятностей попадания значений исследуемой величины в k указанных интервалах (две гистограммы в одних осях).
7. Проведите сравнение экспериментального и теоретического распределений по критерию Пирсона. 8. Проведите проверку нормальности распределения по критериям асимметрии и эксцесса. 9. Проведите проверку двух выборочных совокупностей по критерию Стьюдента и решите вопрос о принадлежности их к одной генеральной совокупности. 10. Сделайте вывод: достигнута ли цель работы, является ли распределение нормальным. Дайте теоретическое обоснование работы, опираясь на вопросы для самоподготовки
Вопросы для самоподготовки: 1. Вероятность случайного события. 2. Статистические показатели выборочной совокупности. 3. Схема предварительной обработки экспериментальных данных. 4. Критерии проверки нормальности распределения.
Литература: 1. Ремизов А.Н. Медицинская и биологическая физика.-М: Дрофа 2011 2. Лекции..
|


 . Результаты занесите в таблицу
. Результаты занесите в таблицу

 и погрешность его определения Δμэфф
и погрешность его определения Δμэфф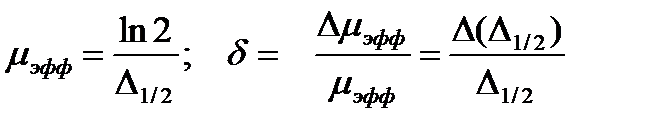
 ,т.е. с погрешностью определения процентной дозы
,т.е. с погрешностью определения процентной дозы 
 Отложив погрешность ± ΔD50% на оси D% вокруг точки D 50%, спроектировать через график погрешность на ось толщины поглотителя. Это и есть погрешность слоя половинного поглощения (Δ(Δ1/2).
Отложив погрешность ± ΔD50% на оси D% вокруг точки D 50%, спроектировать через график погрешность на ось толщины поглотителя. Это и есть погрешность слоя половинного поглощения (Δ(Δ1/2).

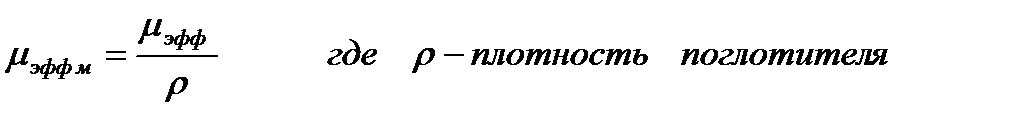
 от xmin до xmax разбейте на k равных интервалов длиной:
от xmin до xmax разбейте на k равных интервалов длиной:


 Нижние границы последующего интервала равны верхним границам предыдущего.
Нижние границы последующего интервала равны верхним границам предыдущего. и среднее арифметическое значение исследуемой величины Х для каждого интервала:
и среднее арифметическое значение исследуемой величины Х для каждого интервала:






 3. Вычислите математическое ожидание исследуемой
3. Вычислите математическое ожидание исследуемой 4. Вычислите дисперсию и среднее квадратическое отклонение по формуле:
4. Вычислите дисперсию и среднее квадратическое отклонение по формуле: 5. Вычислите для каждого интервала параметры Z1, Z2 по формуле:
5. Вычислите для каждого интервала параметры Z1, Z2 по формуле: значений Z (Приложение, таблица2).
значений Z (Приложение, таблица2).







