Третий закон термодинамики
Расчеты изменения энтропии в различных процессах основаны на использовании выражений (2.5)–(2.6) и частных производных энтропии по термодинамическим переменным:
1) Фазовые превращения (переходы) К фазовым превращениям (переходам) относятся процессы плавления, испарения, сублимации и полиморфные превращения. Предполагая, что все эти процессы протекают термодинамически обратимо при постоянном давлении и температуре, для изменения энтропии имеем:
Если фазовый переход происходит при температуре, отличной от температуры обратимого фазового перехода, то использовать формулу (2.10) нельзя (так как для необратимых процессов имеем неравенство (2.3)). В таких случаях для расчета энтропии используют ее свойства как функции состояния, рассматривая цикл:
2) Нагревание или охлаждение при постоянном давлении (объеме) Количество теплоты, необходимое для изменения температуры системы при р = const, выражают с помощью теплоемкости: δQ обр = CpdT. С учетом соотношения (2.5):
Если теплоемкость не зависит от температуры в интервале от Т 1 до Т 2, то уравнение (2.11) можно проинтегрировать: При более сложной температурной зависимости теплоемкости в выражении (3.12) появляются дополнительные слагаемые. Например, если теплоемкость описывается рядом (1.20), то соответствующее изменение энтропии
Изменение энтропии при поглощении теплоты при постоянных температуре и давлении рассчитывают по формуле:
Если изменения происходят при постоянном объеме, то в формулах (2.11) и (2.12) Cр надо заменить на CV, а в формуле (1.5) Qp на QV. В случае, когда нижним пределом интегрирования является абсолютный нуль температуры, выражение (2.11) можно преобразовать к виду
Значение постоянной интегрирования S 0 устанавливается третьим законом термодинамики: при нулевой абсолютной температуре энтропия любых веществ, находящихся в равновесном состоянии, имеет одно и то же значение, не зависящее от фазового состояния вещества. В содержание третьего закона термодинамики входят тепловая теорема Нернста и постулат Планка. В. Нернст, изучая работу гальванических элементов при низких температурах, высказал предположение о том, что вблизи абсолютного нуля все процессы (в том числе и химические реакции) в конденсированных телах должны протекать без изменения энтропии и теплоемкости системы. Так как при 0 К энтропия всех веществ одинакова, то конкретное значение S 0 несущественно и его можно принять равным нулю (постулат Планка): при абсолютном нуле все идеальные кристаллы имеют одинаковую энтропию, равную нулю. Если при нагревании в интервале температур от Т 1 до Т 2 происходят фазовые превращения (например, плавление и испарение), то комбинируя уравнения (2.10) и (2.11) получим:
В уравнении (2.16) Т 2 > Т 1. Если Т 2 < Т 1 (процесс охлаждении), порядок расположения членов в правой части уравнения (2.16) меняется на обратный (первый член становится последним и т. д.). При этом следует учесть, что В соответствии с выражением (2.16) процесс нагревания от Т 1 до Т 2 можно разделить на последовательные стадии: нагревание твердого тела от Т 1 до Т пл (Δ S 1), плавление твердого тела (Δ S 2), нагревание жидкости от Т пл до Т кип (Δ S 3), испарение жидкости при Т кип (Δ S 4), наконец, нагревание пара (газа) от Т кип до Т 2 (Δ S 5). Общее изменение энтропии при изменении температур от Т 1 до Т 2 равно сумме изменений энтропии в отдельных, следующих друг за другом стадиях данного процесса. Тогда выражение (2.10) можно записать в следующем виде:
Постулат Планка позволяет ввести понятие абсолютной энтропии вещества, т. е. энтропии, отсчитанной от нулевого значения при Т = 0, для этого в уравнении (2.16) полагаем
В термодинамических таблицах обычно приводят значения абсолютной энтропии в стандартном состоянии при температуре 298 К или табулируют значения S с шагом по температуре 100 К. 3) Процессы, протекающие в идеальном газе Расчет основан на использовании соотношений Максвелла (2.8) и (2.9):
Так, для изотермического расширения идеального газа с уравнением состояния p = nRT / V:
Этот же результат можно получить, если использовать выражение для теплоты изотермического обратимого расширения идеального газа (табл. 1.1). Формулы для расчета изменения энтропии процессов расширения и сжатия идеального газа при различных условиях представлены в табл. 2.1. Таблица 2.1.
|











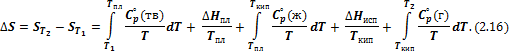
 , а
, а  .
.
 :
:






