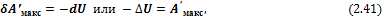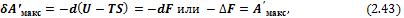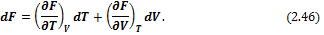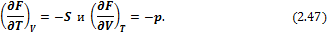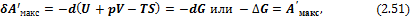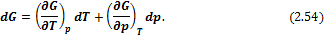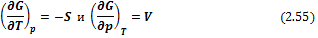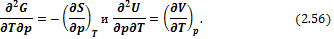Характеристические функции. Вывод уравнений Максвелла. Термодинамические потенциалы
Подставим выражение (2.5) в уравнение (1.1); если речь идет о равновесном процессе, то при отсутствии любого вида работы, кроме работы расширения, можем записать:
Поскольку U – функция состояния, т. е. dU равн. = dU неравн., то уравнение (2.22) применимо безотносительно к тому, равновесно или не равновесно осуществляется процесс. Уравнение (2.28) является обобщенной формой записи первого и второго законов термодинамики. Если (2.28) разрешить относительно энтропии, то получим соотношение
Уравнения (2.28) и (2.29) называют фундаментальными уравнениями Гиббса, они являются характеристическими, т.е. в них в явном виде представлена вся термодинамическая информация о системе; аналогично, функции S (U, V) и U (S, V) называют характеристическими функциями, а соответствующие им наборы переменных – естественными. Характеристической функцией называется функция состояния, посредством которой (и частных производных разных порядков ее по соответствующим ей переменным) могут быть наиболее просто и притом в явном виде выражены все термодинамические свойства системы. Уравнение (2.28) показывает, что U является функцией энтропии и объема системы, т. е. U = f (S, V). Тогда
Сравнивая (2.30) и (2.28), можно констатировать, что
Таким образом, внутренняя энергия является характеристической функцией и ее частные производные выражают параметры системы. Исходя из (2.31), можно записать:
откуда следует, что
Уравнение (2.33) называется первым уравнением Максвелла. Поскольку H = U + pV, тогда dH = dU + pdV, подставим это выражение в (2.28)
Таким образом, энтальпия является характеристической функцией энтропии и давления: H = f (S, p). Тогда
Сравнивая (2.35) и (2.34), получим
Исходя из (2.36), можно записать:
откуда следует, что
Соотношение (2.38) называется вторым уравнением Максвелла. В общем случае уравнение (2.28), объединяющее первое и второе начала термодинамики, можно записать в виде
откуда
где Из (2.40) вытекает наличие характеристических функций состояния системы, убыль которых в обратимом процессе, протекающем при постоянстве определенной пары термодинамических параметров, равна максимальной полезной работе. По аналогии с механикой, где работа постоянно действующих сил также определяется независящей от пути разностью потенциалов этих сил в начальном и конечном состояниях системы, эти функции называются термодинамическими потенциалами. В зависимости от условий протекания процесса различают четыре термодинамических потенциала. 1) При V, S = const уравнение (2.40) принимает вид
т. е. внутренняя энергия является изохорно-изоэнтропийным потенциалом. 2) При р, S = const из уравнения (2.40) находим, что
т. е. энтальпия является изохорно-изоэнтропийным потенциалом. Большинство реальных процессов протекают в условиях, когда S ≠ const и dS ≠ 0. Поэтому с практической точки зрения наибольший интерес представляют изохорно-изотермический и изобарно-изотермический потенциалы. 3) При V, Т = const уравнение (2.40) принимает вид
где величина F = U – TS: является свойством системы; она называется энергией Гельмгольца (функция введена Гельмгольцем в 1882 г.) или изохорно-изотермическим (изохорным) потенциалом. Очевидно, что
Исходя из определения энергии Гельмгольца и уравнения (3.28) получим
Следовательно F является функцией температуры и объема системы: F = f (T, V). Тогда
Сравнивая (2.46) и (2.45), получим
или
Следовательно,
Соотношение (2.49) называется третьим уравнением Максвелла. Объединяя (2.44) и (2.47) получим уравнение Гиббса-Гельмгольца для зависимости Δ F от температуры:
4) При p, Т = const уравнение (2.40) принимает вид
где величина G = U – TS + pV = H – TS = F + pV: является свойством системы; она называется энергией Гиббса (функция введена Гиббсом в 1875 г.) или изобарно-изотермическим (изобарным) потенциалом. Очевидно, что
Исходя из определения энергии Гиббса и уравнения (2.28), получим
Таким образом, G = f (T, р)есть характеристическая функция системы:
Сравнивая (2.54) и (2.53), получим
или
Следовательно,
Соотношение (2.57) является четвертым уравнением Максвелла. Объединяя (2.57) и (2.52) получим уравнение Гиббса-Гельмгольца для зависимости Δ G от температуры:
Любой термодинамический потенциал в необратимых процессах при постоянстве естественных переменных уменьшается и достигает минимума при равновесии. Таким образом, все мыслимые процессы в системах охватываются соотношением:
где знак равенства относится к состоянию равновесия; знак «<» к условию протекания самопроизвольного процесса.
|



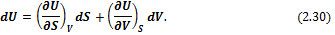
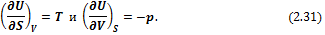
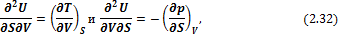


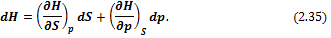
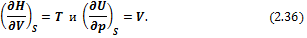
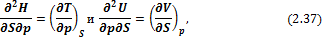

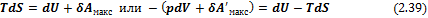

 – максимальная полезная работа (работа против электрических, магнитных и прочих сил); pdV – работа, затраченная на расширение (сжатие) и необходимая для поддержания в данное мгновение в системе давление р.
– максимальная полезная работа (работа против электрических, магнитных и прочих сил); pdV – работа, затраченная на расширение (сжатие) и необходимая для поддержания в данное мгновение в системе давление р.