Формирование реализаций случайных векторов и функций
При использовании метода моделирования часто возникает необходимость в формировании реализаций случайных векторов и случайных процессов, обладающих заданными вероятностными характеристиками. Для получения возможных значений случайного вектора можно воспользоваться различными приемами. Рассмотрим сначала соотношения, аналогичные (1.3). Пусть требуется получить последовательность возможных значений
Выберем из совокупности случайных чисел с равномерным распределением в интервале (0, 1) число Затем найдем условное распределение случайной величины
Выберем из совокупности случайных чисел с равномерным распределением в интервале (0, 1) число Аналогичные соотношения можно записать и для многомерных векторов. Например, если задано совместное распределение
Практическое использование рассмотренных соотношений для получения составляющих случайного вектора связано с весьма громоздкими вычислениями, за исключением тех сравнительно редких случаев, когда интегралы вида (1.2) берутся в конечном виде. Поэтому, как правило, для этой цели приходится пользоваться различными приближенными приемами. В двумерном случае можно считать приемлемым следующий приближенный прием. Рассматривается функция плотности Все перечисленные функции плотности аппроксимируются кусочно-постоянными функциями в соответствии с методикой, рассмотренной выше.
|

 ,
,  — составляющих
— составляющих  случайного вектора, заданных совместной функцией плотности
случайного вектора, заданных совместной функцией плотности  . Найдем частную функцию плотности случайной величины
. Найдем частную функцию плотности случайной величины 
 .
. и одним из способов, рассмотренных выше, определим соответствующее ему число
и одним из способов, рассмотренных выше, определим соответствующее ему число  имеющее функцию плотности
имеющее функцию плотности  .
.
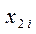 и определим соответствующее ему число
и определим соответствующее ему число 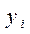 , имеющее функцию плотности
, имеющее функцию плотности  . Легко показать, что каждая из пар получаемой таким образом последовательности
. Легко показать, что каждая из пар получаемой таким образом последовательности  , то случайные числа
, то случайные числа 
 ,
, ,
, .
. и совокупность функций плотности
и совокупность функций плотности  для заранее определенного набора значений
для заранее определенного набора значений  .
.


