Моделирование случайных чисел с равномерным законом распределения
Пример моделирования случайных чисел с равномерным законом распределения приведен в Задании 1.1.: 1. В ячейки А3-А22 записывают номера изготавливаемых деталей от 1 до 20. 2. В ячейки В3-F22 записывают случайные числа с помощью датчика случайных чисел с равномерным законом распределения [0,1] - СЛЧИС(). 3. В ячейки G3-K22 записывают значения центрированной случайной величины c равномерным законом распределения - случайные числа в диапазоне [-1, +1] - 4. В ячейки L3-P22 записывают значения случайной величины c равномерным законом распределения - случайные числа в диапазоне [-5, +15](1.1) - 5. В ячейках F, K, P 23-28 рассчитывают оценки математического ожидания, дисперсии, среднеквадратического отклонения, половины поля рассеяния, минимального и максимального значений массивов В3-F22, G3-K22 и L3-P22. 6. В ячейки Q3-Q12 записывают интервалы значений случайной величины c равномерным законом распределения [0,1] с шагом – 0,1. В ячейки R3-R12 записывают интервалы значений центрированной случайной величины c равномерным законом распределения [-1,+1]с шагом – 0,2. В ячейки S3-S12 записывают интервалы значений случайной величины c равномерным законом распределения [-5,+15] с шагом – 2. 7. В ячейки T3-T13 записывают расчетные значения частот попадания случайной величины c равномерным законом распределения [0,1], полученные с помощью функции ЧАСТОТА =ЧАСТОТА(B3:F22;Q3:Q12). 8. В ячейки U3-U13 записывают расчетные значения частот попадания случайной величины c равномерным законом распределения [-1,+1], полученные с помощью функции ЧАСТОТА =ЧАСТОТА(G3:K22;R3:R12). 9. В ячейки V3-V13 записывают расчетные значения частот попадания случайной величины c равномерным законом распределения [-5,+15], полученные с помощью функции ЧАСТОТА =ЧАСТОТА(L3:P22;S3:S12). 10. Гистограммы частот T3-T13, U3-U13, V3-V13 распределений случайных величин выводят на графики (см. приложение 3).
|

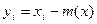 . В данном случае
. В данном случае  .
. . В данном случае
. В данном случае  .
.


