Свойства равномерного распределения.
Непрерывная случайная величина
Функция распределения случайной величины
Рис.1.1. Плотности распределения вероятностей: а) общий случай; б) центрированная случайная величина в диапазоне (-1,+1) Математическое ожидание М [
В частном случае равномерного распределения в интервале (0, 1) случайная величина
функцию распределения
а математическое ожидание и среднее квадратическое отклонение соответственно равны
Данная случайная величина часто используется для реализации датчиков случайных чисел. В МS Ехсеl такой датчик выполнен в виде функции СЛЧИС, которая при обращении к ней выдает случайные числа в интервале (0, 1). При моделировании случайных чисел удобно использовать центрированную случайную величину с равномерным законом распределения в диапазоне (-1,+1) (рис.1.1б)
Пример моделирования случайных чисел с равномерным законом распределения приведен в Задании 1.1.
Формирование возможных значений случайных величин с
|
имеет равномерное распределение в интервале 
(рис. 1.1а), если ее функция плотности равна
.
соответственно равны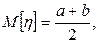
,
,
.
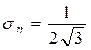, с помощью которой можно легко моделировать случайные числа 
с математическим ожиданием 
в диапазоне (а, b)
. (1.1)
