Формирование случайных чисел с нормальным законом распределения с использованием предельных теорем теории вероятностей
Пример моделирования случайных чисел с нормальным законом распределения на основе моделировании условий предельной теоремы теории вероятностей приведен в Задании 1.5. Для улучшения асимптотической нормальности случайных чисел используются специальные преобразования (1.10), (1.11). 1. В ячейки А3-E42 записывают 5 рядов по 40 случайных чисел с помощью датчика случайных чисел с равномерным законом распределения [0,1] - СЛЧИС(). 2. В ячейки F3-F42 записывают случайные числа, полученные путем суммирования 5-ти случайных чисел с равномерным законом распределения (1.8) с математическим ожиданием 3. В ячейки G3-G42 записывают случайные числа, полученные согласно соотношению (1.9) - 4. В ячейки H3-H42 записывают случайные числа, полученные согласно соотношению (1.10) - 5. В ячейки I3-I42 записывают случайные числа, полученные согласно соотношению (1.11) - 6. В ячейках F, G, H, I 43-46 рассчитывают оценки математического ожидания, дисперсии, среднеквадратического отклонения, половины поля рассеяния значений массивов F3-F42, G3-G42, H3-H42, I3-I42. 7. В ячейки J3-J15 записывают интервалы значений случайных величин c шагом – 0,05. 8. В ячейки K3-K16 записывают расчетные значения частот попадания случайной величины (1.9) - 9. В ячейки L3-L16 записывают расчетные значения частот попадания случайной величины (1.10) - 10. В ячейки M3-M16 записывают расчетные значения частот попадания случайной величины (1.11) - 11. В ячейки N3-N16 записывают расчетные значения интегральных частот попадания случайной величины, распределенной по нормальному закону в соответствие с функцией =НОРМРАСП(J3;$G$43;$G$45;1), где J3 –значения абсолютной частоты в интервале; $G$43 – оценка математического ожидания массива данных G3-G42; $G$45 – оценка среднеквадратического отклонения массива данных G3-G42; 1 – постоянная определяющая расчет интегральных частот попадания случайной величины, распределенной по нормальному закону. 12. В ячейки О3-О16 записывают расчетные значения абсолютных частот попадания случайной величины, распределенной по нормальному закону - 13. В ячейки Р3-Р16 записывают расчетные значения абсолютных частот попадания случайной величины, распределенной по нормальному закону для 40 испытаний - 14. В ячейки К19, записывают расчетные значения функции =ХИ2ТЕСТ(K3:K15;P3:P15), L19 - =ХИ2ТЕСТ(L3:L15;P3:P15), M19- =ХИ2ТЕСТ(M3:M15;P3:P15), определяющие вероятность совпадения наблюдаемых (фактических) абсолютных частот попадания случайных величин в массивах K3-K16, L3-L16, M3-M16, абсолютным частотам нормального закона для 40 испытаний приведенных в массиве Р3-Р16. 15. Гистограммы абсолютных частот K3-K16, L3-L16, M3-M16, N3-N16, O3-O16, P3-P16 распределений случайных величин выводят на графики (см. приложение 3).
|

 и средним квадратическим отклонением
и средним квадратическим отклонением  .
. , где
, где  - случайные числа, полученные помощью датчика случайных чисел с равномерным законом распределения, в ячейках А3-E42 – в диапазоне [0,1] - СЛЧИС().
- случайные числа, полученные помощью датчика случайных чисел с равномерным законом распределения, в ячейках А3-E42 – в диапазоне [0,1] - СЛЧИС().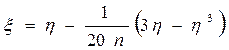 .
. .
. , c нормальным законом распределения, полученные с помощью функции ЧАСТОТА =ЧАСТОТА(G3:G42;J3:J15).
, c нормальным законом распределения, полученные с помощью функции ЧАСТОТА =ЧАСТОТА(G3:G42;J3:J15). , c нормальным законом распределения, полученные с помощью функции ЧАСТОТА =ЧАСТОТА(H3:H42;J3:J15).
, c нормальным законом распределения, полученные с помощью функции ЧАСТОТА =ЧАСТОТА(H3:H42;J3:J15).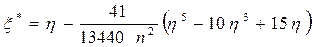 , c нормальным законом распределения, полученные с помощью функции ЧАСТОТА =ЧАСТОТА(I3:I42;J3:J15).
, c нормальным законом распределения, полученные с помощью функции ЧАСТОТА =ЧАСТОТА(I3:I42;J3:J15).
 .
.


