В качестве примера использования предельных теорем рассмотрим получение случайных чисел, имеющих закон распределения Пуассона
 с математическим ожиданием
с математическим ожиданием 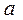 .
.
Для этого воспользуемся предельной теоремой Пуассона: если 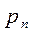 — вероятность наступления события А при одном испытании, то вероятность наступления
— вероятность наступления события А при одном испытании, то вероятность наступления 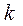 событий в
событий в 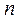 независимых испытаниях при
независимых испытаниях при  ,
,  ,
, 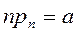 асимптотически равна (7).
асимптотически равна (7).
Выберем достаточно большое 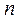 , такое, чтобы
, такое, чтобы
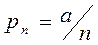
оказалось меньшим единицы. Будем проводить серии по 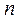 независимых испытаний, в каждом из которых событие А происходит с вероятностью
независимых испытаний, в каждом из которых событие А происходит с вероятностью 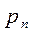 , и подсчитывать число
, и подсчитывать число 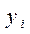 - случаев фактического наступления события А в серии с номером i. Числа
- случаев фактического наступления события А в серии с номером i. Числа 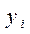 , будут приближенно следовать закону Пуассона, причем тем точнее, чем больше
, будут приближенно следовать закону Пуассона, причем тем точнее, чем больше 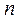 . Практически
. Практически 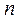 должно выбираться таким образом, чтобы
должно выбираться таким образом, чтобы 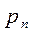 было не более 0,1… 0,2.
было не более 0,1… 0,2.
Машинная процедура получения последовательности случайных чисел состоит в следующем.
Из совокупности случайных чисел с равномерным распределением в интервале (0, 1) выбирается число  и сравнивается с
и сравнивается с 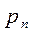 . Если
. Если 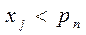 , к содержимому специальной ячейки (которая носит название «счетчик числа событий») прибавляется единица, а если
, к содержимому специальной ячейки (которая носит название «счетчик числа событий») прибавляется единица, а если  , прибавляется нуль.
, прибавляется нуль.
После проведения 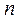 испытаний такого рода содержимое счетчика числа событий считывается и используется в качестве случайного числа с законом распределения Пуассона.
испытаний такого рода содержимое счетчика числа событий считывается и используется в качестве случайного числа с законом распределения Пуассона.

 с математическим ожиданием
с математическим ожиданием 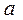 .
.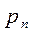 — вероятность наступления события А при одном испытании, то вероятность наступления
— вероятность наступления события А при одном испытании, то вероятность наступления 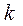 событий в
событий в 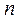 независимых испытаниях при
независимых испытаниях при  ,
,  ,
, 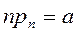 асимптотически равна (7).
асимптотически равна (7).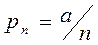
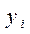 - случаев фактического наступления события А в серии с номером i. Числа
- случаев фактического наступления события А в серии с номером i. Числа  и сравнивается с
и сравнивается с 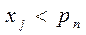 , к содержимому специальной ячейки (которая носит название «счетчик числа событий») прибавляется единица, а если
, к содержимому специальной ячейки (которая носит название «счетчик числа событий») прибавляется единица, а если  , прибавляется нуль.
, прибавляется нуль.


