Использованием предельных теорем теории вероятностей. Например, пусть требуется получить последовательность случайных чисел , имеющих нормальное распределение с математическим ожиданием и средним
Например, пусть требуется получить последовательность случайных чисел
Здесь можно воспользоваться центральной предельной теоремой теории вероятностей и построить случайные числа Так как исходным материалом для суммирования служат случайные числа, имеющие равномерное распределение в интервале (0, 1), то мы можем воспользоваться центральной предельной теоремой для одинаково распределенных случайных величин: если независимые случайные величины
асимптотически нормальна с математическим ожиданием Как показывают расчеты, сумма Как известно, математическое ожидание для случайных величин, имеющих равномерное распределение в интервале (0, 1), равно 0,5, а среднее квадратическое отклонение Поэтому сумма Для обеспечения достаточно точного совпадения закона распределения суммы (1.8) с нормальным, очевидно, требуется увеличивать число слагаемых Как показано в работе [3], для улучшения асимптотической нормальности случайных чисел можно воспользоваться специальными преобразованиями. Так, если имеется сумма
случайных величин
будет иметь распределение, достаточно близкое к нормальному, при Еще более точным в этом смысле является преобразование
для которого, по-видимому, достаточно иметь Практическое использование преобразований вида (1.10) и (1.11) может оказаться весьма полезным при решении многих задач. Окончательное мнение о целесообразности выбора определенного значения
|

 , имеющих нормальное распределение с математическим ожиданием
, имеющих нормальное распределение с математическим ожиданием  и средним квадратическим отклонением
и средним квадратическим отклонением 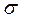
 .
. имеют все одно и то же распределение вероятностей и если каждое
имеют все одно и то же распределение вероятностей и если каждое  имеет математическое ожидание
имеет математическое ожидание  и среднее квадратическое отклонение
и среднее квадратическое отклонение  , то сумма
, то сумма (1.8)
(1.8)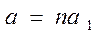 и средним квадратическим отклонением
и средним квадратическим отклонением  .
. имеет распределение, близкое к нормальному, уже при сравнительно небольших
имеет распределение, близкое к нормальному, уже при сравнительно небольших  . Практически для получения последовательности нормально распределенных случайных чисел можно пользоваться значениями
. Практически для получения последовательности нормально распределенных случайных чисел можно пользоваться значениями  .
. и среднее квадратическое отклонение
и среднее квадратическое отклонение  .
. (1.9)
(1.9) равномерно распределенных в интервале
равномерно распределенных в интервале  , то величина
, то величина (1.10)
(1.10) оказывается заведомо близким к нормальному.
оказывается заведомо близким к нормальному. , (1.11)
, (1.11)


