ПРИМЕР 1. Контракт предусматривает следующий порядок использования кредитной линии: 01.07.96 г
Контракт предусматривает следующий порядок использования кредитной линии: 01.07.96 г. — 5 млн. руб., 01.01.97 г. — 15 млн. руб., 01.01.99 г. — 18 млн. руб. Необходимо определить сумму задолженности на начало 2000 г. и современную стоимость этого потока на начало срока при условии, что проценты начисляются по ставке 20% годовых. Находим S = 5х1,23,5 +15 х 1,23 +18 х 1,2 = 56,985 млн. руб. По этим же данным определим современную стоимость потока на момент выплаты первой суммы. При прямом счете получим A = 5 + 15х1,2-0,5+18х1,2-2,5 = 30,104 млн. руб. или по формуле (1.5) А = 56,985 х 1,2-3,5 = 56,985 х 0,52828 = 30,104 млн. руб. Забегая вперед, заметим, что в практике анализа производственных инвестиций занял видное место показатель, названный чистым приведенным доходом (net present value, NPV). Он представляет собой современную стоимость потока платежей, характеризующего инвестиционный процесс в целом. Таким образом, NPV равен величине А, определенной по формуле (1.2). Поскольку, как было сказано выше, члены такого потока могут быть как положительными, так и отрицательными величинами, то NPV также может иметь тот или другой знак. Отрицательная величина означает, что получаемые доходы с учетом временного фактора не окупают инвестиционные затраты при заданном уровне процентной ставки. Ограничимся пока данным замечанием. (Подробно сущность этого важнейшего показателя и методы его расчета для различных видов потоков платежей рассмотрены в гл. 5.) Формулы для расчета обобщающих параметров постоянных дискретных рент. Для потоков платежей в виде постоянных рент расчеты современных стоимостей и наращенных сумм можно существенно упростить, применяя стандартные формулы. При их записи используем следующие обозначения: А — современная стоимость ренты; S — наращенная сумма ренты; R — член ренты (размер платежа); п — срок ренты; р — число выплат в году; i — процентная ставка; v — дисконтный множитель по ставке i (1.3). Ниже приводятся формулы для наиболее распространенных видов рент[3]. Во всех случаях предполагаются сложные процентные ставки. Постоянная годовая рента постнумерандо. Современная стоимость ренты:
Множитель, на который умножается R, называется коэффициентом приведения ренты, обозначим его an;i:
Значения an;i табулированы[4]. Краткая таблица коэффициентов приведения имеется в Приложении (табл. 2). Отметим некоторые свойства этого коэффициента. Чем выше значение i, тем меньше его величина (рис 1.1). При i = 0 an;i = п. В свою очередь, при увеличении срока ренты величина an;i растет и стремится к некоторому пределу (рис 1.2). При п = ∞; предельное значение коэффициента составит:
Коэффициент приведения (1.8) применяется при расчете современной стоимости вечной ренты. Наращенная сумма постоянной ренты определяется по формуле
Множитель, на который умножается R, называется множителем наращения ренты. Обозначим его sn;i:
Значения этого множителя нетрудно табулировать для необходимых диапазонов ставок и сроков[5] — см. Приложение (табл. 1).
|

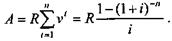 (1.6)
(1.6) (1.7)
(1.7)
 (1.8)
(1.8) (1.9)
(1.9)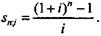 (1.10)
(1.10)


