ПРИМЕР 11
Пусть в примере 9 дисконтирование осуществляется по силе роста, равной 10%, тогда, используя (1.25), получим Сила роста, эквивалентная дискретной ставке 10%, составит: Непрерывно изменяющийся поток платежей. Выше предполагалось, что годовая сумма R непрерывно и равномерно распределена в пределах года. Такой поток денежных поступлений или выплат не является единственно возможным. На практике, особенно при анализе инвестиций в производство, поток платежей может существенно изменяться во времени, в том числе и следуя какой-либо закономерности, например если ожидается, что в течение первых трех лет работы произойдет плавное и непрерывное увеличение выпуска продукции с постоянным темпом прироста. Если поток платежей непрерывен и описывается функцией rt = f (t), то общая сумма поступлений за время п равна Причем зависимость между А и S можно представить как
Чтобы рассчитать величины А и S, необходимо определить конкретный вид функции изменения платежей и значения ее параметров. Рассмотрим методы расчета современных стоимостей только для двух видов функций — линейной и экспоненциальной. Линейно изменяющийся непрерывный поток платежей. Функция такого потока Rt =R0+at, где R 0 — начальный размер платежа, выплачиваемого в единицу времени, в котором измеряется срок ренты; а — прирост в единицу времени. Современная стоимость получена с помощью интегрирования функции потока платежей:
где
|


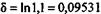 , или 9,531%. Откуда
, или 9,531%. Откуда  т. е. получен тот же результат, что и в примере 9.
т. е. получен тот же результат, что и в примере 9. . В этом случае современная стоимость и наращенная сумма (при начислении процентов используется процентная ставка в виде силы роста) находятся как
. В этом случае современная стоимость и наращенная сумма (при начислении процентов используется процентная ставка в виде силы роста) находятся как 
 (1.27)
(1.27)
 — коэффициент приведения постоянной непрерывной ренты (см. (1.25)).
— коэффициент приведения постоянной непрерывной ренты (см. (1.25)).


