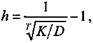ПРИМЕР 15Облигация со сроком 5 лет, проценты по которой выплачиваются один раз в год по норме 8%, куплена по курсу 97. Запишем уравнение эквивалентности (1.32) и разделим обе его стороны на 100: 0,97 = (1 + j)-5 + 0,08 a 5; j . С помощью линейной интерполяции находим j = 8,77%. Для проверки рассчитаем курс на основе полученной ставки. Находим
Как видим, расчетный курс весьма близок к рыночному 97. Приближенное решение по (1.33) дает
что соответствует рыночному курсу 0,74. Погрешность заметно выше, чем при использовании линейной интерполяции. Уравнение эквивалентности для третьей схемы (ежегодные выплаты сумм обслуживания долга без льготного периода) имеет вид:
где Dt — остаток долга на начало года t, D 1 = D, Dt = Dt- 1- d. Для быстрой ориентации в сложившейся ситуации иногда прибегают к приближенному методу оценки доходности как суммы двух составляющих:
где h — доходность от разности номинала и цены; i — процентная ставка по условиям финансового инструмента. При определении первого элемента этой суммы фактический процесс последовательного погашения долга условно заменяется разовым погашением со средним сроком выплаты. Из равенства K = DvT следует, что
где Т — средний срок. Средний срок в данной ситуации определяется элементарно: Т =п/ 2. Наличие льготного периода (без погашения основного долга) увеличивает средний срок на соответствующую величину.
|
(1.34)
— годовой размер погашения долга;
