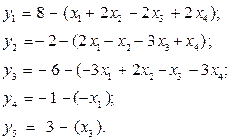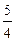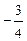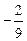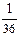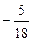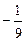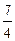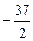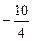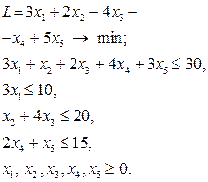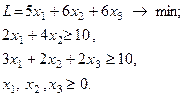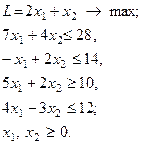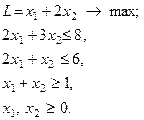Алгоритм розв’язання задачі лінійного програмування за допомогою симплекс-методу
Алгоритм симплекс-методу дозволяє повністю дослідити ЗЛП. Якщо розв’язок існує, то його буде знайдено симплекс-процедурою, якщо розв’язку немає то в процесі реалізації симплекс-процедури буде встановлено факт його відсутності. Схема розв’язання має такий вигляд. І. Згідно [1], записуємо ЗЛП (5.1), (5.2) в нормальному стандартному вигляді.
ІІ. Будуємо симплекс-таблицю.
Змінні Суть симплекс-методу полягає у взаємозаміні базових змінних на вільні за спеціальною (описаною нижче) процедурою для одержання спочатку допустимого, а потім і оптимального розв’язку задачі. Розв’язок називатимемо допустимим, якщо він задовольняє нерівності (5.2). ІІІ. Шукаємо допустимий розв’язок. Для цього побудуємо нову симплекс-таблицю (7.3), згідно наступних правил: 1. Беремо будь-який від’ємний елемент у першому стовпчику таблиці (7.2) (за винятком першого). Якщо такого елемента немає, переходимо до виконання пункту ІV. Нехай таким елементом є bm < 0. 2. У рядку, де знаходиться вибраний елемент (у цьому прикладі рядок m) вибираємо будь-який від’ємний елемент (якщо такий є). Стовпчик з цим елементом призначаємо базовим. Якщо від’ємного елемента в рядку немає, вибираємо інший рядок з від’ємним елементом у першому стовпчику. Якщо у всіх рядках від’ємних елементів немає, то й задача розв’язку не має. Область порожня. 3. У базовому стовпчику перебираємо всі елементи (крім першого), які мають однакові знаки з відповідними елементами першого стовпчика. Для них обчислюємо відношення 4. У базовій клітинці таблиці (7.3) записуємо елемент обернений до відповідного елемента табл. (7.2). 5. Усі елементи базового рядка ділимо на цей елемент, але обчислень ніяких не виконуємо; 6. Усі елементи базового стовпчика ділимо на базовий елемент, а результат записуємо з протилежним знаком. 7. Усі інші елементи табл. (7.3) утворюються як результат додавання відповідного елемента табл. (7.2) та добутку відповідного елемента базового стовпчика табл. (7.3) на чисельник відповідного елемента базового рядка тієї самої таблиці.
8. Після заповнення табл. (7.3), повторюємо процедуру починаючи з 9. Процедуру повторюємо доти, доки в першому стовпчику останньої таблиці (за винятком першого, знак якого не враховується) не зникнуть від’ємні елементи. ІV. Будуємо оптимальний розв’язок ЗЛП 1. Знаходимо серед елементів першого рядка (крім першого елемента) додатні числа. Якщо таких елементів немає, переходимо до виконання 2. Стовпчик, де знаходиться шуканий додатний елемент (будь-який з них), позначаємо базовим. Далі повторюємо процедуру п. ІІІ починаючи з підпункту 3 доти, доки не зникнуть додатні елементи в першому рядку. Якщо в першому рядку додатних елементів немає, переходимо до виконання наступного пункту. V. Усі вільні змінні (змінні, які стоять у верхній частині останньої симплекс-таблиці) покладаємо рівними нулю. Усі базові змінні (змінні, які стоять у лівій частині таблиці) покладаємо відповідно числам, які стоять у першому стовпчику останньої симплекс-таблиці. означає, що змінна, яка стоїть у першому рядку таблиці (після Зауваження 1. Якщо в задачі (5.1), (5.2)
а в першій симплекс-таблиці перший рядок матиме такий вигляд:
Кінцева таблиця симплекс-процедури І-V у першій клітинці міститиме число, яке дорівнює Зауваження 2. Якщо під час виконання пункту IV з’являється ситуація, коли перший рядок симплекс-таблиці містить додатні елементи, а в стовпчику, де вони містяться, додатних елементів немає, тоді й задача розв’язку не має, область необмежена і розв’язок знаходиться в нескінченності. Приклад. Розв’язати ЗЛП
за умов
Розв’язування: Запишемо задачу в нормальному вигляді (виконаємо п. І).
Складаємо симплекс-таблицю:
Визначаємо базовий стовпчик і базовий рядок, перетин яких дає базовий елемент. Базовий елемент «-1». Будуємо нову таблицю.
Повторюємо симплекс-процедуру.
Записуємо фінальну симплекс-таблицю:
Відповідь: Завдання для самостійних і контрольних робіт Розв’язати за допомогою симплекс-методу:
|

 (7.1)
(7.1)
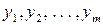 назвемо базовими змінними; змінні
назвемо базовими змінними; змінні  – вільними змінними. Узагалі кажучи, змінні, які стоять у лівій частині будемо називати базовими, ті, що стоять у правій верхній частині, – вільними.
– вільними змінними. Узагалі кажучи, змінні, які стоять у лівій частині будемо називати базовими, ті, що стоять у правій верхній частині, – вільними. , j0 – номер базового стовпчика. Нехай j0 =2
, j0 – номер базового стовпчика. Нехай j0 =2 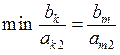 , тоді m рядок призначаємо базовим, а елемент am2, який стоїть у клітинці, де перетинаються базовий рядок і базовий стовпчик,– базовим елементом. Проводимо взаємозаміну вільної та базової змінних, які відповідають базовому стовпчику та базовому рядку.
, тоді m рядок призначаємо базовим, а елемент am2, який стоїть у клітинці, де перетинаються базовий рядок і базовий стовпчик,– базовим елементом. Проводимо взаємозаміну вільної та базової змінних, які відповідають базовому стовпчику та базовому рядку. виписуємо з таблиці (7.2).
виписуємо з таблиці (7.2).






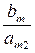




 ) покладається рівною першому числу цього рядка першого стовпчика, друга змінна – другому числу першого стовпчика і т.д.
) покладається рівною першому числу цього рядка першого стовпчика, друга змінна – другому числу першого стовпчика і т.д.  покладається рівним
покладається рівним  , де
, де  тоді в (7.1) перша нерівність виглядатиме так:
тоді в (7.1) перша нерівність виглядатиме так: ,
,