Економічна інтерпретація основної та спряженої задач лінійного програмування
Основну ЗЛП (8.1), (8.2) можна інтерпретувати так. Нехай є n різних технологій для виробництва одного продукту. При цьому використовується m інгредієнтів (різні види сировини й інші виробничі фактори). За j-ю технологієюза одиницю часу використовується Природно виникає задача: відшукати такий оптимальний план, при якому за наявних запасів інгредієнтів виготовлялася б максимальна кількість продукції. Математична модель цієї ситуації – основна ЗЛП: максимізувати лінійну форму
за обмежень
Для економічної інтерпретації спряженої ЗЛП зручно ціну одиниці продукції, що виготовляється, узяти за одиницю. Тоді за j- ю технологією за одиницю часу створюється продукт ціною в
Зрозуміло, що
Отже, математичною моделлю економічної задачі встановлення у взятому масштабі таких допустимих цін на інгредієнти, щоб ціна їх резерву була найменшою, слугує спряжена задача: мінімізувати лінійну форму
за обмежень
Тепер властивість 1 (розд. 8) набуває економічної суті: якщо для задачі (8.1), (8.2) існує оптимальний план максимального виготовлення продукції, то існує й оптимальний план мінімальних відносних цін на інгредієнти. Причому в цьому масштабі цін сумарна вартість усієї продукції, виготовленої за оптимальним планом, збігається із сумарною вартістю Властивість 2 можна трактувати так: якщо в деякому оптимальному плані виробництва витрати
то в кожному оптимальному плані відносних цін ціна
Далі, якщо в деякому оптимальному плані відносних цін сумарна вартість
то в жодному оптимальному плані виробництва j- та технологія не використовується, тобто
Отже, оптимальні плани спряжених задач становлять гармонію: оптимальному плану виробництва відповідає оптимальний план відносних цін, за яким використовувані технології рентабельні, а ті, що не використовуються, збиткові, і навпаки.
|

 одиниць і- го інгредієнта, загальний запас якого дорівнює
одиниць і- го інгредієнта, загальний запас якого дорівнює  і виробляється
і виробляється  одиниць продукту. Нехай
одиниць продукту. Нехай  – час, протягом якого виробництво здійснюється за j- ю технологією. Тоді при «завданні»
– час, протягом якого виробництво здійснюється за j- ю технологією. Тоді при «завданні»  буде вироблено
буде вироблено  одиниць продукції і використано
одиниць продукції і використано  одиниць і- го інгредієнта (
одиниць і- го інгредієнта (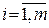 ).
).
 одиниць першого інгредієнта,
одиниць першого інгредієнта,  – другого інгредієнта,....,
– другого інгредієнта,....,  – m- го інгредієнта. Позначивши відносні ціни одиниці кожного інгредієнта відповідно
– m- го інгредієнта. Позначивши відносні ціни одиниці кожного інгредієнта відповідно  для оцінки використаних ресурсів (у прийнятому масштабі цін) одержимо суму
для оцінки використаних ресурсів (у прийнятому масштабі цін) одержимо суму 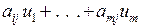 і очевидно, вона не менша за ціну
і очевидно, вона не менша за ціну  (9.1)
(9.1) і, що взявши достатньо великі
і, що взявши достатньо великі  , ми задовольняємо всі умови. Не бажаючи, одначе, завищувати відносні ціни інгредієнтів, можна взяти їх меншими, щоб подальше їх зниження було неможливим (оскільки умова (9.1) перестане виконуватись). За мінімальних відносних цін інгредієнтів, ціна всього запасу набуватиме найменше значення і складе суму
, ми задовольняємо всі умови. Не бажаючи, одначе, завищувати відносні ціни інгредієнтів, можна взяти їх меншими, щоб подальше їх зниження було неможливим (оскільки умова (9.1) перестане виконуватись). За мінімальних відносних цін інгредієнтів, ціна всього запасу набуватиме найменше значення і складе суму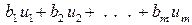



 запасів всіх інгредієнтів.
запасів всіх інгредієнтів. і- го інгредієнта строго менші за його резерви
і- го інгредієнта строго менші за його резерви  :
: ,
, цього інгредієнта дорівнює нулю. Якщо ціна
цього інгредієнта дорівнює нулю. Якщо ціна 
 інгредієнтів, що використовуються за j- ю технологією, строго більша за ціну
інгредієнтів, що використовуються за j- ю технологією, строго більша за ціну  ,
, Якщо ж за деяким оптимальним планом j- та технологія використовується (
Якщо ж за деяким оптимальним планом j- та технологія використовується ( ), то в кожному оптимальному плані відносних цін ціна
), то в кожному оптимальному плані відносних цін ціна 



