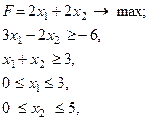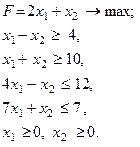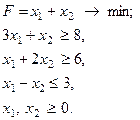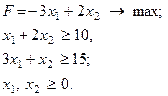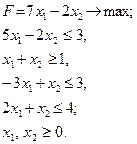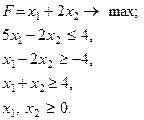Приклад. Знайти найбільше та найменше значення функції

якщо х1 та х2 задовольняють нерівностям (лежать в області D1):
 (6.1)
(6.1)
Розв’язування:  – нормалі до прямих, які утворені заміною знаків «≤;» та «≥;» на знак «=».
– нормалі до прямих, які утворені заміною знаків «≤;» та «≥;» на знак «=».  – нормаль до прямої
– нормаль до прямої 
Будуємо область D1 (рис. 1).

Рис. 1
Алгоритм побудови області D1, може бути таким:
- Будуємо прямокутник Р: (
 ).
).
2. У побудованому прямокутнику шукаємо точки, які задовольняють першу нерівність  Для цього будуємо пряму
Для цього будуємо пряму  за двома точками перетину з осями координат (0, 6) та (6, 0). Пряма ділить прямокутник Р на дві частини. Та частина прямокутника, яка лежить у напрямку
за двома точками перетину з осями координат (0, 6) та (6, 0). Пряма ділить прямокутник Р на дві частини. Та частина прямокутника, яка лежить у напрямку  від прямої, має значення лівої частини рівності більші за 6 (у напрямку нормалі лінійна функція
від прямої, має значення лівої частини рівності більші за 6 (у напрямку нормалі лінійна функція  зростає), але щоб задовольнити першу нерівність треба розглядати всі значення х1 та х2 для яких ліва частина нерівності менша за 6. Цю умову буде виконано якщо в прямокутнику Р узяти частину, яка лежить на самій прямій та в напрямку антинормалі
зростає), але щоб задовольнити першу нерівність треба розглядати всі значення х1 та х2 для яких ліва частина нерівності менша за 6. Цю умову буде виконано якщо в прямокутнику Р узяти частину, яка лежить на самій прямій та в напрямку антинормалі  . Тобто, щоб задовольнити першу нерівність, треба брати точки прямокутника Р, які лежать на прямій
. Тобто, щоб задовольнити першу нерівність, треба брати точки прямокутника Р, які лежать на прямій  і нижче від неї.
і нижче від неї.
3. В одержаному чотирикутнику (трапеції), слід залишити лише ті точки, які задовольняють другу з нерівностей (6.1): 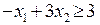 . Аналогічно, як і в попередньому пункті, будуємо пряму
. Аналогічно, як і в попередньому пункті, будуємо пряму 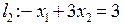 . Точки, що нас цікавлять (де
. Точки, що нас цікавлять (де 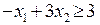 ) лежать в напрямку нормалі до прямої l2,
) лежать в напрямку нормалі до прямої l2,  та на самій прямій.
та на самій прямій.
4. В одержаному трикутнику слід вилучити точки, які не задовольняють умову  (третій нерівності в (6.1)). Будуємо пряму
(третій нерівності в (6.1)). Будуємо пряму  і вибираємо точки на прямій та поза прямою в бік антинормалі
і вибираємо точки на прямій та поза прямою в бік антинормалі  . Одержимо знову чотирикутник (див. рис. 1).
. Одержимо знову чотирикутник (див. рис. 1).
5. Завершуємо побудову області D1, вилученням з одержаного чотирикутника точок, що не задовольняють нерівності  . Це точки, які лежать поза прямою
. Це точки, які лежать поза прямою  в напрямку антинормалі
в напрямку антинормалі  . Одержуємо п’ятикутник АВСDE. Переходимо до виконання пункту 2.
. Одержуємо п’ятикутник АВСDE. Переходимо до виконання пункту 2.
Шукаємо оптимальні розв’язки.
1. 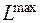 знаходиться в крайній точці області D1, в напрямку нормалі
знаходиться в крайній точці області D1, в напрямку нормалі  до L,
до L,  .
.
2.  знаходиться в крайній точці області D1 в напрямку антинормалі
знаходиться в крайній точці області D1 в напрямку антинормалі  . Крайньою точкою області D1 будемо називати точку у якій перетинаються пряма
. Крайньою точкою області D1 будемо називати точку у якій перетинаються пряма  з областю так, що будь-яке зміщення цієї прямої в окіл точки (в напрямку
з областю так, що будь-яке зміщення цієї прямої в окіл точки (в напрямку  ) спричиняє відсутність на прямій точок області D1; d – величина (відстань) на яку зміщується пряма
) спричиняє відсутність на прямій точок області D1; d – величина (відстань) на яку зміщується пряма  в напрямку нормалі або антинормалі.
в напрямку нормалі або антинормалі.
 знаходиться шляхом обчислення функції L у точці перетину прямих l2 та l3 (напрям
знаходиться шляхом обчислення функції L у точці перетину прямих l2 та l3 (напрям  ). Точку перетину знаходять як результат розв’язку системи рівнянь
). Точку перетину знаходять як результат розв’язку системи рівнянь 
 – значення функції L у точці перетину осі х2 з прямою l1 (напрям
– значення функції L у точці перетину осі х2 з прямою l1 (напрям  ). Точку перетину знаходять через розв’язання системи рівнянь
). Точку перетину знаходять через розв’язання системи рівнянь 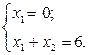
Відповідь:  .
.
Завдання для самостійних і контрольних робіт
Розв’язати графічно ЗЛП.
| 1.
| 
| 2.
| 
|
| 3.
| 
| 4.
| 
|
| 5.
| 
| 6.
| 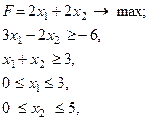
|
| 7.
| 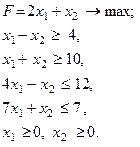
| 8.
| 
|
| 9.
| 
| 10.
| 
|
| 11.
| 
| 12.
| 
|
| 13.
| 
| 14.
| 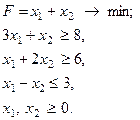
|
| 15.
| 
| 16.
| 
|
| 17.
| 
| 18.
| 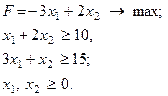
|
| 19.
| 
| 20.
| 
|
| 21.
| 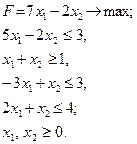
| 22.
| 
|
| 23.
| 
| 24.
| 
|
| 25.
| 
| 26.
| 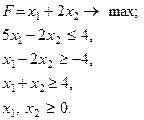
|
| 27.
| 
|
| 
|
| 29.
| 
| 30.
| 
|
| 31.
| 
| 32.
| 
|


 (6.1)
(6.1) – нормалі до прямих, які утворені заміною знаків «≤;» та «≥;» на знак «=».
– нормалі до прямих, які утворені заміною знаків «≤;» та «≥;» на знак «=».  – нормаль до прямої
– нормаль до прямої 

 ).
). Для цього будуємо пряму
Для цього будуємо пряму  за двома точками перетину з осями координат (0, 6) та (6, 0). Пряма ділить прямокутник Р на дві частини. Та частина прямокутника, яка лежить у напрямку
за двома точками перетину з осями координат (0, 6) та (6, 0). Пряма ділить прямокутник Р на дві частини. Та частина прямокутника, яка лежить у напрямку  від прямої, має значення лівої частини рівності більші за 6 (у напрямку нормалі лінійна функція
від прямої, має значення лівої частини рівності більші за 6 (у напрямку нормалі лінійна функція  зростає), але щоб задовольнити першу нерівність треба розглядати всі значення х1 та х2 для яких ліва частина нерівності менша за 6. Цю умову буде виконано якщо в прямокутнику Р узяти частину, яка лежить на самій прямій та в напрямку антинормалі
зростає), але щоб задовольнити першу нерівність треба розглядати всі значення х1 та х2 для яких ліва частина нерівності менша за 6. Цю умову буде виконано якщо в прямокутнику Р узяти частину, яка лежить на самій прямій та в напрямку антинормалі  . Тобто, щоб задовольнити першу нерівність, треба брати точки прямокутника Р, які лежать на прямій
. Тобто, щоб задовольнити першу нерівність, треба брати точки прямокутника Р, які лежать на прямій 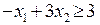 . Аналогічно, як і в попередньому пункті, будуємо пряму
. Аналогічно, як і в попередньому пункті, будуємо пряму 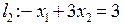 . Точки, що нас цікавлять (де
. Точки, що нас цікавлять (де  та на самій прямій.
та на самій прямій. (третій нерівності в (6.1)). Будуємо пряму
(третій нерівності в (6.1)). Будуємо пряму  і вибираємо точки на прямій та поза прямою в бік антинормалі
і вибираємо точки на прямій та поза прямою в бік антинормалі  . Одержимо знову чотирикутник (див. рис. 1).
. Одержимо знову чотирикутник (див. рис. 1). . Це точки, які лежать поза прямою
. Це точки, які лежать поза прямою  в напрямку антинормалі
в напрямку антинормалі  . Одержуємо п’ятикутник АВСDE. Переходимо до виконання пункту 2.
. Одержуємо п’ятикутник АВСDE. Переходимо до виконання пункту 2.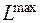 знаходиться в крайній точці області D1, в напрямку нормалі
знаходиться в крайній точці області D1, в напрямку нормалі  до L,
до L,  .
. знаходиться в крайній точці області D1 в напрямку антинормалі
знаходиться в крайній точці області D1 в напрямку антинормалі  . Крайньою точкою області D1 будемо називати точку у якій перетинаються пряма
. Крайньою точкою області D1 будемо називати точку у якій перетинаються пряма  з областю так, що будь-яке зміщення цієї прямої в окіл точки (в напрямку
з областю так, що будь-яке зміщення цієї прямої в окіл точки (в напрямку  ) спричиняє відсутність на прямій точок області D1; d – величина (відстань) на яку зміщується пряма
) спричиняє відсутність на прямій точок області D1; d – величина (відстань) на яку зміщується пряма  в напрямку нормалі або антинормалі.
в напрямку нормалі або антинормалі. знаходиться шляхом обчислення функції L у точці перетину прямих l2 та l3 (напрям
знаходиться шляхом обчислення функції L у точці перетину прямих l2 та l3 (напрям 
 – значення функції L у точці перетину осі х2 з прямою l1 (напрям
– значення функції L у точці перетину осі х2 з прямою l1 (напрям  ). Точку перетину знаходять через розв’язання системи рівнянь
). Точку перетину знаходять через розв’язання системи рівнянь 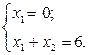
 .
.