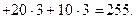Задачі транспортного типу
Викладений у попередніх розділах симплекс-метод універсальний для розв’язання ЗЛП і може використовуватися для будь-яких задач такого типу. Він дозволяє повністю дослідити ЗЛП: знайти розв’язок, якщо він існує, або встановити факт його відсутності. Проте існують окремі випадки ЗЛП, які через внутрішні особливості задачі (властивості коефіцієнтів цільової функції Класична ЗТТ формулюється таким чином. Нехай є m пунктів відправлення продукції:
Будемо вважати, що задано вартість перевезень
Треба скласти такий план перевезень, щоб забезпечити виконання всіх замовлень і щоб сумарна вартість перевезень при цьому була мінімальна (найменша):
де Побудуємо математичну модель цієї задачі. Невід’ємні змінні 1. Сумарна величина вантажу, який направляється з кожного пункту відправлення в усі пункти призначення, має дорівнювати запасам вантажу в даному пункті.
або
2. Сумарна кількість вантажу, що перевозиться в кожний пункт призначення з усіх пунктів відправлення, має дорівнювати замовленню для даного пункту. Це дає нам n умов-рівностей:
або
3. Має виконуватись умова (10.2):
Функція Як і будь-яку ЗЛП, її можна було б розв’язати використовуючи симплекс-метод, але внутрішня специфіка задачі (обмеження-рівності, одиничні коефіцієнти в обмеженнях, невід’ємність коефіцієнтів Неважко переконатися, що не всі n+m рівнянь (10.3), (10.4) незалежні. Дійсно, підсумовуючи всі рівняння (10.3) та (10.4) одержимо одне й теж саме число згідно з умовою (10.1). Отже, умови (10.3), (10.4) зв’язані однією лінійною залежністю, і фактично з цих рівнянь лише n+m-1, не n+m, лінійно незалежні. Це означає, що ранг системи рівнянь (10.3), (10.4) однаковий: r = n+m-1, а отже, можна розв’язати ці рівняння відносно n+m-1 базових змінних, виразивши їх через інші, вільні. Підрахуємо кількість вільних змінних: k = mn-(m+n-1) = mn – m - (n-1) = (m-1)(n-1). Із розгляду ЗЛП відомо, що оптимальний розв’язок досягається в одній з вершин області допустимих розв’язків (ОДР), де хоча б k змінних перетворюється на нуль. У нашому випадку для оптимального плану перевезень хоча б (m-1)(n-1) значень Будь-яку сукупність План Допустимий план будемо називати опорним, якщо в ньому відмінні від нуля не більше r = n+m-1 базових перевезень План Розв’язок ЗТТ можна звести до деякої маніпуляції із симплекс-таблицями, які для цієї задачі будемо називати транспортними таблицями,
де ПП – пункт призначення вантажу; ПВ – пункт відправлення вантажу; усі інші позначення відповідають попереднім. Клітинки таблиці, у яких будемо записувати відмінні від нуля перевезення, називатимемо базовими, а Отже, розв’язок задачі зводиться до знаходження додатних чисел, які, будучи поставлені в базових клітинках транспортної таблиці, забезпечили б виконання таких умов: сума перевезень у кожному рядку таблиці має дорівнювати запасу даного ПВ; сума перевезень у кожному стовпчику таблиці має дорівнювати розміру замовлення певного ПП; сумарна вартість перевезень – мінімальна. Надалі всі дії щодо знаходженню розв’язків ЗТТ будуть пов’язані з перетвореннями транспортної табл. (10.6). Для опису цих перетворень скористаємося нумерацією клітинок таблиці, подібної до нумерації клітин шахової дошки. Клітинкою ( 11. Знаходження опорного плану Розв’язок ЗТТ, як і кожної ЗЛП починається із знаходження опорного (допустимого) розв’язку, або, як будемо говорити, опорного плану. На відміну від загального випадку ЗЛП розв’язок ЗТТ завжди існує, оскільки сумарна вартість перевезень Покажемо, як можна побудувати опорний план перевезення вантажу. Для цього використовують різні способи. Зупинимося на найпростішому, який називається методом північно-західного кута. Пояснимо його суть на конкретному прикладі. Приклад. Розглянемо таблицю:
Розв’язування. Перепишемо табл. (11.1) і будемо поступово заповнювати її перевезеннями, починаючи з лівої верхньої клітинки (1,1) (північно-західного кута таблиці). Міркуємо таким чином. Пункт В1 подав замовлення на 18 одиниць вантажу. Задовольнимо це замовлення за рахунок запасу 48, який є в пункті А1, і запишемо перевезення 18 в клітинці (1,1). Після цього замовлення з пункту В1 виконане, а в пункті А1 залишилося ще 48-18=30 одиниць продукції. Задовольняємо за їх рахунок замовлення з пункту В2 (27 одиниць). Запишемо 27 в клітинку (1,2). Три одиниці продукції в пункті А1 призначимо пункту В3. У складі замовлення В3 залишилися незабезпеченими 39 одиниць. З них 30 покриємо за рахунок пункту А2, чим його запас буде вичерпано, а ще 9 візьмемо з пункту А3. Із 18 одиниць пункту відправлення А3 12 виділимо на пункт В4; 6 одиниць, що лишилися, призначимо пункту В5 і разом з 20 одиницями пункту А4 повністю покриємо його замовлення. Одержимо:
Таким чином, складено план перевезень, що задовольняє балансові рівняння вигляду (10.3), (10.4). Одержаний розв’язок не тільки допустимим, а й опорний розв’язок ЗТТ. Клітинки таблиці (11.2), в яких стоять ненульові перевезення – базові, їх кількість задовольняє умову r= n+m-1=8. Інші клітинки – вільні (порожні), їх кількість (m-1)(n-1)=12. Отже, план опорний і поставлене завдання побудови опорного плану виконане. Виникає запитання: а чи оптимальний за сумарною вартістю перевезень план отримано? Звичайно, ні. Адже під час побудови опорного плану зовсім не враховувалась вартість локальних перевезень
Не важко переконатися, що коли перенесемо 18 одиниць з клітини (1,1) в клітину (2,1), а потім 18 одиниць з клітини (2,3) в (1,3), одержимо сумарну вартість перевезень:
Балансові співвідношення при цьому не були порушені. Отже, попередній план перевезень не був оптимальним. 12. Поліпшення плану перевезень Візьмемо транспортну таблицю, яка складається із 5 рядків та 6 стовпчиків (кількість рядків і стовпчиків не суттєва).
Домовимося відмічати знаком «+» ті вершини циклу, перевезення в яких збільшуються, а знаком «–» – вершини, в яких вони зменшуються. Цикл з вершинами, відміченими знаками «+» або «–», будемо називати орієнтованим. Знаки «+» та «–» у циклі будемо розставляти почергово, це означає, що у вершини зі знаком «+» дві сусідні мають знаки «–» і навпаки. Перенести якусь кількість одиниць вантажу орієнтованим циклом означає збільшити перевезення у вершинах зі знаком «+», і зменшити перевезення на ту саму кількість вантажу у вершинах зі знаком «–». Очевидно, що з перенесенням будь-якої кількості одиниць вантажу по циклу рівновага між запасами і замовленнями зберігається: сума перевезень у кожному рядку дорівнює запасам цього рядка, а сума перевезень у кожному стовпчику дорівнює замовленню по цьому стовпчику. Отже, за будь-якого циклічного перенесення, що залишає перевезення невід’ємними, допустимий (опорний) план залишається допустимим (опорним). Сумарна вартість усього плану перевезень може змінюватися – збільшуватися або зменшуватися. Назвемо ціною циклу збільшення вартості перевезень із переміщенням одиниці вантажу означеним циклом. Очевидно, ціна циклу дорівнює алгебраїчній сумі вартостей, що стоять у вершинах циклу. Вартості, що стоять у вершинах циклу зі знаком «+» беруться із знаком «+», а ті, що стоять у вершинах із знаком «–», беруться зі знаком «–». Наприклад, для циклів зображених в табл. (12.1), ціна циклів відповідно дорівнює: с21 – с2 3+ с43 – с41 і с14 – с16 + с46 – с44 + с34 – с35 + с55 – с54. Позначимо ціну циклу через r. Із переміщенням одиниці вантажу по циклу вартість перевезення збільшиться на величину r; із переміщенням по ньому k одиниць вантажу вартість перевезень збільшиться на kr. Звідси випливає: щоб поліпшити план перевезень, треба здійснювати перевезення тими циклами, ціна яких від’ємна. Якщо кожного разу вдасться здійснити таке переміщення, то вартість плану зменшиться на величину kr. Оскільки перевезення не можуть бути від’ємними, будемо користуватися лише тими циклами, «від’ємні» вершини яких лежать у базових клітинках таблиці. Якщо циклів з від’ємними числом r у таблиці не залишилося, це означає, що подальше поліпшення плану не можливе, тобто задачі (10.3), (10.4), (10.5) розв’язані. Відшукати цикли з від’ємними вартостями можна використовуючи метод потенціалів. Будемо вважати, що кожен із пунктів відправлення Аі вносить на перевезення одиниці вантажу (все одно куди) якусь суму
будемо називати Позначимо всю сукупність платежів Теорема 1. Для заданої сукупності платежів
за будь-якого допустимого плану перевезень (
У цій формулі величина С залежить лише від сукупності платежів Доведемо це твердження. Маємо
Перетворимо першу з двох останніх сум
відповідно до рівностей (10.3). Аналогічно
в силу рівностей (10.4). Таким чином,
Останній вираз для Спробуємо встановити зв’язок між вартостями та псевдовартостями. Припустимо, що план (
Для довільних клітин (
Співвідношення між Теорема 2. Якщо в усіх базових клітинках (
а для всіх вільних клітинок (
то план перевезень оптимальний і ніяким способом не може бути здешевлений. Доведення. Позначимо через У сумі (12.4) відмінні від нуля лише доданки, які відповідають базовим клітинкам, але в них вартості дорівнюють псевдовартостям (згідно з (12.2)). Тому Згідно з теоремою 1
де
згідно (12.3). Тому сума (12.5)
Звідси випливає, що в умовах теореми 2 ніякими змінами плану перевезень ( Не важко переконатися, що дана теорема справедлива також для виродженого плану, у якому деякі з базових змінних дорівнюють нулю. Дійсно, те, що в базових клітинках перевезення строго додатні, для доведення не суттєво: достатньо, щоб вони були невід’ємними. Таким чином, доведено, що ознакою оптимальності плану (
План, для якого виконуються ці умови називається потенціальним, а відповідні платежі Для розв’язання ЗТТ треба побудувати потенціальний план. Його можна побудувати методом послідовних наближень, задаючись спочатку довільною системою платежів, які задовольняють першу з умов (12.6). Причому в кожній базовій клітинці призначимо суму платежів, що дорівнює вартості перевезень у цій клітинці, потім будемо поліпшувати план, змінюючи систему платежів так, щоб вони наближались до потенціальних. Для поліпшення плану перевезень використаємо властивість платежів і псевдовартостей: яка б не була система платежів
Приклад. Розглянемо таблицю:
Візьмемо будь-яку вільну клітинку, наприклад (1,5), і побудуємо її цикл перерахунку, додатна вершина якого лежить у вільній клітинці, а всі інші – в базових. Визначимо вартість циклу:
Відповідно до умов (12.6) для всіх базових клітинок вартість дорівнює псевдовартостям, тому
Очевидно, що ця властивість справедлива для будь-якої довільної клітинки. Крім того, вона спрощує пошук циклів з від’ємною вартістю. Процедура побудови потенціального плану така: як перше наближення до оптимального плану береться будь-який допустимий план. Платежі
Рівнянь у (12.9) m+n-1, а кількість невідомих m+n, отже, одну з невідомих можна взяти довільною (наприклад, нульовою), а інші визначимо із системи:
то план перевезень не оптимальний і може бути поліпшений перенесенням перевезень по циклу, який відповідає вільній клітинці. Вартість циклу встановлюється за формулою (12.7). Алгоритм розв’язання ЗТТ методом потенціалів (на підставі теореми 2) такий: 1. Беремо будь-який опорний план перевезень, у якому відмічено m+n-1 базових клітинок (інші клітинки – вільні). 2. Визначаємо для цього плану платежі
один з платежів можна призначити довільно, наприклад, покласти рівним нулю. 3. Перераховуємо псевдовартість 4. Якщо хоча б в одній вільній клітинці псевдовартість більша за вартість, необхідно поліпшити план, перерозподіливши перевезення по циклу, який відповідає будь-якій вільній клітинці з від’ємною вартістю циклу. 5. Знову перераховуємо платежі і псевдовартості, і якщо план усе ще не оптимальний, продовжуємо процедуру поліпшення доти, доки не буде знайдено оптимальний план. Приклад. Розв’язати ЗТТ методом потенціалів, якщо опорний план побудовано за допомогою методу північно-західного кута.
Псевдовартості
Отримаємо вісім рівнянь і дев’ять невідомих, тому маємо право одну з невідомих покласти рівною нулю (
Оскільки не всі псевдовартості у вільних клітинках табл. (12.11) задовольняють умову (12.6), план наведений в таблиці не оптимальний. Спробуємо його поліпшити, переводячи в базову одну з вільних клітинок, для якої Знову повторимо перетворення в таблиці, перерахувавши псевдовартості після заміни в (12.12) рівняння
Відповідь:
Поняттям «платежі» та «псевдовартості» можна дати наочну економічну інтерпретацію. Будемо вважати, що Розв’яжемо методом потенціалів ЗТТ у виродженому випадку. Приклад. Розв’язати ЗТТ, транспортна таблиця якої має вигляд (12.16). Будемо вважати, що опорний план методом північно-західного кута побудували.
Після застосування методу північно-західного кута до нової таблиці, отримаємо табл. (12.17).
Після побудови потенціального плану в табл. (12.20) покладемо ε =0. Відповідь:
|

 , матриці обмежень
, матриці обмежень  , правих частин b та ін.) допускають розв’язання простішими методами. До них належать і задачі транспортного типу (ЗТТ).
, правих частин b та ін.) допускають розв’язання простішими методами. До них належать і задачі транспортного типу (ЗТТ).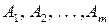 , у яких сконцентровано запаси певного однорідного товару (вантажу) в кількості відповідно
, у яких сконцентровано запаси певного однорідного товару (вантажу) в кількості відповідно  одиниць. Крім того, є n пунктів призначення:
одиниць. Крім того, є n пунктів призначення:  , які подали замовлення відповідно на
, які подали замовлення відповідно на 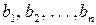 одиниць товару. Припустімо, що сума всіх замовлень дорівнює сумі запасів:
одиниць товару. Припустімо, що сума всіх замовлень дорівнює сумі запасів: (10.1)
(10.1)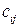 одиниці товару від кожного пункту відправлення
одиниці товару від кожного пункту відправлення  до кожного пункту призначення
до кожного пункту призначення  . Матрицю (таблицю) перевезень
. Матрицю (таблицю) перевезень 
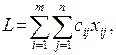 (10.2)
(10.2)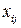 – кількість товару, що перевозиться з пункту
– кількість товару, що перевозиться з пункту  в пункт
в пункт  (кількість яких
(кількість яких 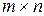 ) повинні задовольняти такі умови:
) повинні задовольняти такі умови:
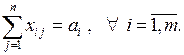 (10.3)
(10.3)
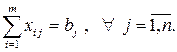 (10.4)
(10.4) (10.5)
(10.5)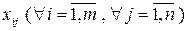 будемо називати планом перевезень, або просто планом.
будемо називати планом перевезень, або просто планом. будемо називати допустимим, якщо він задовольняє умови (10.3), (10.4) ( «балансові умови» – всі замовлення виконані, всі запаси вичерпані).
будемо називати допустимим, якщо він задовольняє умови (10.3), (10.4) ( «балансові умови» – всі замовлення виконані, всі запаси вичерпані).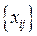 , а всі інші дорівнюють нулю.
, а всі інші дорівнюють нулю.
 ), або
), або 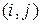 , будемо називати клітинку, яка стоїть в i- му рядку і j- му стовпчику транспортної таблиці. Наприклад, верхня ліва клітинка позначатиметься як (1, 1), яка стоїть під нею – (1,2) і т.д.
, будемо називати клітинку, яка стоїть в i- му рядку і j- му стовпчику транспортної таблиці. Наприклад, верхня ліва клітинка позначатиметься як (1, 1), яка стоїть під нею – (1,2) і т.д.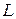 – невід’ємна обмежена знизу функція.
– невід’ємна обмежена знизу функція. .
.
 c14
+
c14
+
 +
+

 , у свою чергу кожен із пунктів призначення
, у свою чергу кожен із пунктів призначення  також вносить за перевезення одиниці вантажу суму
також вносить за перевезення одиниці вантажу суму  . Ці суми передаються третій особі («перевізнику»). Позначимо
. Ці суми передаються третій особі («перевізнику»). Позначимо
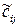 псевдовартістю перевезення одиниці вантажу із пункту
псевдовартістю перевезення одиниці вантажу із пункту  в пункт
в пункт  не обов’язково мають бути додатними: не виключено, що «перевізник» сам платить тому чи іншому пункту якусь премію за перевезення.
не обов’язково мають бути додатними: не виключено, що «перевізник» сам платить тому чи іншому пункту якусь премію за перевезення. ,
,  через
через  . Не уточнюючи, у який спосіб вони призначаються сформулюємо «теорему про платежі».
. Не уточнюючи, у який спосіб вони призначаються сформулюємо «теорему про платежі».
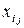 ) зберігає одне й те саме значення:
) зберігає одне й те саме значення: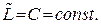

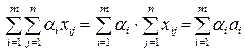
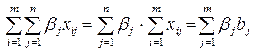
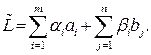
 від (
від (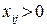 . Визначимо платежі
. Визначимо платежі  при
при  ) співвідношення між
) співвідношення між  та
та 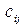 може бути будь-яким:
може бути будь-яким: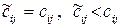 або
або 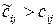 при
при  та
та  у вільних клітинках таблиці показує, чи оптимальний план перевезень обрано і чи можна його поліпшити.
у вільних клітинках таблиці показує, чи оптимальний план перевезень обрано і чи можна його поліпшити. (12.2)
(12.2) (12.3)
(12.3)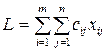 (12.4)
(12.4)
 . Тепер замінимо план (
. Тепер замінимо план ( ). Новий план має сумарну вартість:
). Новий план має сумарну вартість: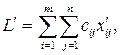 (12.5)
(12.5)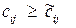

 для всіх базових клітинок;
для всіх базових клітинок;
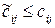 для всіх вільних клітинок.
для всіх вільних клітинок.
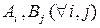 . Теорему 2 можна переформулювати так: будь-який потенціальний план оптимальний.
. Теорему 2 можна переформулювати так: будь-який потенціальний план оптимальний.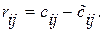 (12.7)
(12.7) –
–
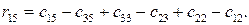


 (12.9)
(12.9)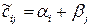 для всіх вільних клітин. Якщо виконується умова
для всіх вільних клітин. Якщо виконується умова  то ЗТТ розв’язана, оскільки план перевезень оптимальний. Якщо ж хоча б в одній вільній клітинці псевдовартість більша за вартість:
то ЗТТ розв’язана, оскільки план перевезень оптимальний. Якщо ж хоча б в одній вільній клітинці псевдовартість більша за вартість: (12.10)
(12.10)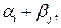 виходячи з умови, що в будь-якій базовій клітинці псевдовартість дорівнює вартості:
виходячи з умови, що в будь-якій базовій клітинці псевдовартість дорівнює вартості:
 – 17
– 17
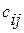 – у правій. Один з платежів, наприклад, αі покладемо рівним нулю (
– у правій. Один з платежів, наприклад, αі покладемо рівним нулю ( ). Для кожної базової клітинки покладемо
). Для кожної базової клітинки покладемо 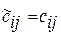 . Випишемо клітинки, де виконується ця рівність:
. Випишемо клітинки, де виконується ця рівність:

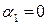 ):
):
 (12.12)
(12.12) , наприклад, клітинку (2,1). Будуємо відповідний цій клітинці цикл (див. табл. (12.11)). Вартість циклу 5 – 8 = –3. Перенесемо по ньому 13 одиниць вантажу(найменше число, що стоїть у вершинах циклу з від’ємними вершинами). Сумарна вартість перевезень зменшилася на
, наприклад, клітинку (2,1). Будуємо відповідний цій клітинці цикл (див. табл. (12.11)). Вартість циклу 5 – 8 = –3. Перенесемо по ньому 13 одиниць вантажу(найменше число, що стоїть у вершинах циклу з від’ємними вершинами). Сумарна вартість перевезень зменшилася на 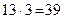 .
.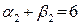 на
на  , перерозв’язавши систему рівнянь.
, перерозв’язавши систему рівнянь. 4 –
4 –
 26 –
26 –
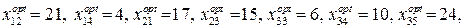
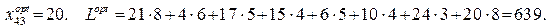
 . Оптимальним буде такий план перевезень, за якого пункти
. Оптимальним буде такий план перевезень, за якого пункти  20 –
20 –
 20+ε –
20+ε –
 –
–