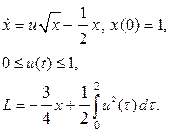Принцип максимуму Л. С. Понтрягіна
Розглянемо математичну модель оптимального керування. Нехай математична модель економічної системи має вигляд:
Будемо вважати, що треба перевести систему за фіксований час Т із стартового стану
де Спряженою до (16.1) будемо називати систему рівнянь:
де H – функція Гамільтона:
Сформулюємо теорему [4]: принцип максимуму Л. С. Понтрягіна. Теорема. Для розв’язання задачі (16.1), (16.2) необхідне виконання умови:
або
при кожному Очевидно, у разі виконання умови (16.4) на єдиному наборі Проілюструємо застосування принципу максимуму на конкретному прикладі. Функції Приклад. Розв’язати макроекономічну задачу оптимального керування [7], якщо модель системи описується диференційним рівнянням вигляду:
де х – відношення основного капіталу до кількості населення; u – частка національного доходу, спрямована на збільшення основного капіталу; n – амортизаційна постійна; Математична модель (16.5) побудована на допущенні, що частка оплати праці дорівнює Задача полягає у знаходженні
де Алгоритм розв’язку задачі: 1. Будуємо функцію Гамільтона для задачі (16.5),(16.6):
де
2. Згідно з принципом максимуму:
Спочатку не будемо зважати на нерівності
Підставимо отримане значення
Отримаємо диференціальне рівняння з відокремлюваними змінними. 3. Розв’яжемо рівняння (16.9)
Враховуючи
Оскільки знайдено 4. Знайдемо траєкторію
Враховуючи початкову умову
Підставляючи значення
Знайдемо розв’язок для кожного з трьох випадків:
Проведемо заміну змінних:
Як і в попередньому випадку покладемо:
Розв’язати задачі оптимального керування.
|

 (16.1)
(16.1)
 –похідна функції x(t) за t.
–похідна функції x(t) за t.  – неперервно-диференційовані функції за фазовими змінними
– неперервно-диференційовані функції за фазовими змінними  ;
;  – вектор-параметр керування, який знаходиться в розпорядженні ОПР.
– вектор-параметр керування, який знаходиться в розпорядженні ОПР. 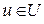 , де U – множина змінних вектор-параметра керування.
, де U – множина змінних вектор-параметра керування. у такий стан
у такий стан 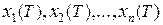 , у якому функціонал:
, у якому функціонал: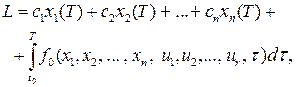 , (16.2)
, (16.2) – диференційована функція аргументів
– диференційована функція аргументів  , досягає найменшого значення. Тобто, треба знайти таке оптимальне керування, набір
, досягає найменшого значення. Тобто, треба знайти таке оптимальне керування, набір  з множини U, і відповідну йому оптимальну траєкторію, що мінімізують функціонал (16.2).
з множини U, і відповідну йому оптимальну траєкторію, що мінімізують функціонал (16.2). (16.3)
(16.3) ,
,  .
. (16.4)
(16.4)
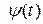 , що задовольняє (16.3).
, що задовольняє (16.3). , та існування розв’язку задачі оптимального керування принцип максимуму є і достатньою умовою оптимальності
, та існування розв’язку задачі оптимального керування принцип максимуму є і достатньою умовою оптимальності  на розв’язках задачі (16.1), (16.3).
на розв’язках задачі (16.1), (16.3). будемо вважати залежними від часу.
будемо вважати залежними від часу. (16.5)
(16.5) – виробнича функція.
– виробнича функція. ;
;  – задані числа,
– задані числа,  .
. , що забезпечує мінімальне значення функціоналу:
, що забезпечує мінімальне значення функціоналу: (16.6)
(16.6) – наперед задані додатні числа.
– наперед задані додатні числа. ,
, (16.7)
(16.7)
 . Тоді:
. Тоді: або
або  (16.8)
(16.8) в (16.7).
в (16.7). (16.9)
(16.9)


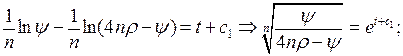


 , отримаємо:
, отримаємо:


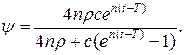
 , для оптимального керування
, для оптимального керування  , що задовольняє принцип максимуму (16.4), то можна вважати
, що задовольняє принцип максимуму (16.4), то можна вважати  .
. , для оптимального керування:
, для оптимального керування:
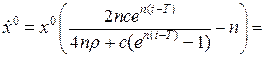






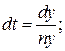

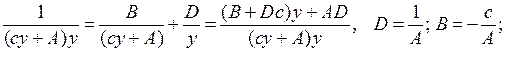




 або
або 




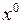 в (16.8) отримаємо
в (16.8) отримаємо






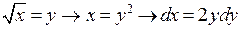










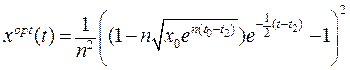
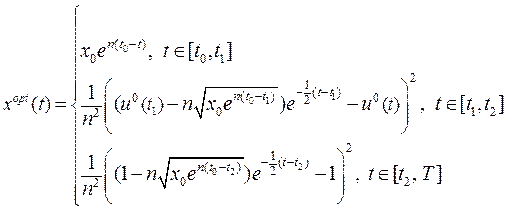 (16.19)
(16.19)