Оптимізація розподілу ресурсів в умовах кризи. Оптимальність за Парето
Будемо вважати, що об’єкт виробничої діяльності складається з керівного центрального органу і S підпорядкованих йому підсистем. Підсистеми зобов’язані виконувати замовлення центрального органу, але після виконання замовлень (за наявності ресурсних можливостей) можуть вести і самостійну господарську діяльність. Замовлення центрального органу має пріоритет. Будемо також вважати, що центральний орган має ресурсні резерви відповідно в кількостях Нехай потреба в продукції, яку виробляє об’єкт економічної діяльності, складається відповідно з вектора чисел
де Викладені вище припущення дозволяють запропонувати таку модель раціонального розподілу запасів ресурсів. Через недостатній рівень запасів вектора
за умови:
Локальна мета кожної з v підсистем прибутку:
за виконання умов:
Нехай Як бачимо, модель багатокритеріальна. Розглянемо наступний алгоритм оптимізації: 1. В нерівностях (17.1), (17.3) зробимо заміну змінних 2. Знайдемо
3. Перевіряємо
Якщо нерівність (17.5) порушується, то запаси ресурсів не забезпечують «виживання» виробництва. У такому випадку слід нарощувати (якщо є така можливість) ті резерви, для яких забезпечується нерівність (17.5). 4. Будемо вважати, що умова (17.4) виконується. Тоді покладемо
5. Розшукаємо такі компоненти в (17.6), які не входять у нерівності (17.1), (17.3) з коефіцієнтом відмінним від нуля. Якщо такі знайшлися, виконуємо п.6. У випадку відсутності шуканих компонентів переходимо до виконання п.7. 6. Знаходимо число
Покладаємо
де 7. Якщо умови п.5 не виконуються, тоді формуємо нерівності:
і розв’язуємо задачу лінійного програмування (17.2), (17.8), послідовно знаходячи Результатом розв’язування даної багатокритеріальної задачі є одержання розв’язку за Парето. Описаний вище алгоритм, поступового покомпонентного наповнення розв’язку задачі особливо ефективний для розв’язування задач великої розмірності на комплексах ЕОМ. Оптимум за Парето означає, що будь-яке відхилення від оптимуму або погіршує значення хоча б одного критерію, або виводить розв’язок за межі області.
|

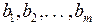 , де m – розміри номенклатури резервів.
, де m – розміри номенклатури резервів. , де
, де  – кількість продукції і-го виду, яку треба виробити. Нормативні затрати резервних ресурсів складають матрицю:
– кількість продукції і-го виду, яку треба виробити. Нормативні затрати резервних ресурсів складають матрицю:
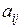 – кількість і-го ресурсу необхідного для випуску одиниці j-го продукту. Вважаємо, що деякі ресурси (резерви) можуть бути поповнені під час виробничої діяльності фірми (економічної системи). Відомі також граничні допустимі норми випуску продукції, які, будучи порушені, призводять до припинення діяльності фірми (нижні границі випуску). Це границі її життєдіяльності. Установлені нормативи затрат ресурсів локальних підсистем. Будемо вважати, що завдання центрального органу не може бути виконане через обмеженість резервів.
– кількість і-го ресурсу необхідного для випуску одиниці j-го продукту. Вважаємо, що деякі ресурси (резерви) можуть бути поповнені під час виробничої діяльності фірми (економічної системи). Відомі також граничні допустимі норми випуску продукції, які, будучи порушені, призводять до припинення діяльності фірми (нижні границі випуску). Це границі її життєдіяльності. Установлені нормативи затрат ресурсів локальних підсистем. Будемо вважати, що завдання центрального органу не може бути виконане через обмеженість резервів. досягнути не можна. Тому логічно поставити задачу: за наявних ресурсів забезпечити найбільший процент виконання плану. Це означає, що треба забезпечити
досягнути не можна. Тому логічно поставити задачу: за наявних ресурсів забезпечити найбільший процент виконання плану. Це означає, що треба забезпечити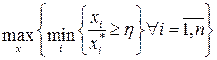
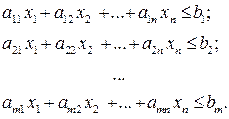 (17.1)
(17.1)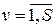 складається з максимізації
складається з максимізації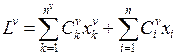 (17.2)
(17.2)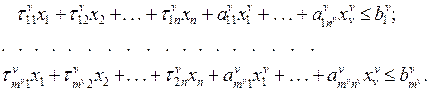 (17.3)
(17.3)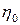 – характеризує границю «живучості» об’єкта виробничої діяльності. Жодного продукту не можна випускати менше пропорції
– характеризує границю «живучості» об’єкта виробничої діяльності. Жодного продукту не можна випускати менше пропорції 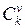 – вартість одиниці продукції відповідної v-ї підсистеми,
– вартість одиниці продукції відповідної v-ї підсистеми, 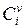 – ціна продукції хі для v-ї підсистеми.
– ціна продукції хі для v-ї підсистеми.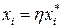 і покладемо
і покладемо 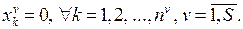
 (17.4)
(17.4) (17.5)
(17.5)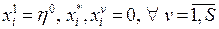 (17.6)
(17.6)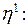
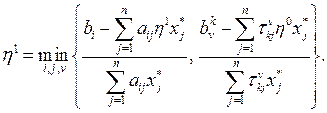
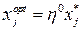 , якщо
, якщо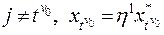 , (17.7)
, (17.7)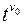 – номер компоненти для якої умова п.5 виконалась. Далі повторюємо виконання п.5 за виконання умови (17.7).
– номер компоненти для якої умова п.5 виконалась. Далі повторюємо виконання п.5 за виконання умови (17.7).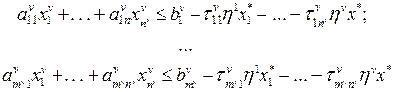 (17.8)
(17.8)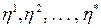 доти, доки перестане виконуватися п.5 (
доти, доки перестане виконуватися п.5 (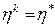 );
); 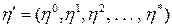 , де компоненти вектора
, де компоненти вектора  характеризують покомпонентні «пороги» значень граничних рівнів виробництва продукції.
характеризують покомпонентні «пороги» значень граничних рівнів виробництва продукції.


