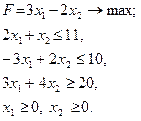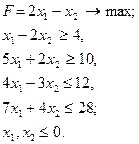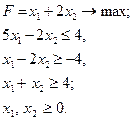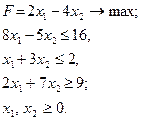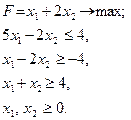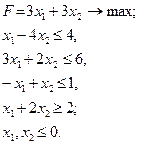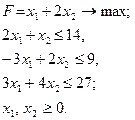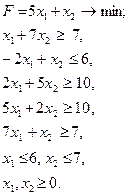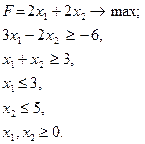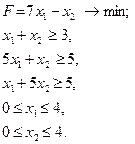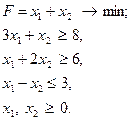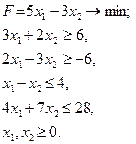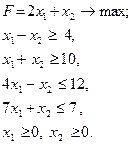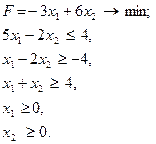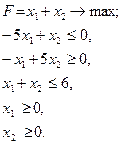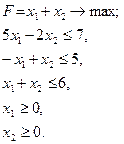Розв’язання задач лінійного програмування в цілих числах
Часто в ЗЛП
за обмежень
потрібно одержати розв’язок у якому деякі або всі компоненти мають бути цілими числами. Для цього використовують метод ланцюгів і границь. Схема розв’язання ЗЛП у цілих числах ЦЗЛП полягає в наступному: 1. Розв’язуємо ЗЛП (14.1), (14.2) за допомогою симплекс-методу (або будь-яким іншим методом) без умови цілочисельності змінних. Якщо змінні – цілі числа, то задачу можна вважати розв’язаною. Нехай змінна xk набула не цілого значення xk=αk, αk має дробову складову. 2. Розв’язуємо дві задачі: a) (14.1), (14.2) за умови b) (14.1), (14.2) за умови де значок 3. У випадку цілих розв’язків задач a) і b) порівнюємо одержані значення функцій L. Більше з них – оптимальне значенням 4. Якщо ж знайдеться таке xl, що не відповідає умові цілочисельності, тоді повторюємо виконання п.2, замінивши xk на xl. Таку процедуру повторюємо доти, доки всі потрібні змінні не стануть цілими. Приклад. Розв’язати ЗЛП в цілих числах:
Розв’язування. Виконуємо п. 1 відповідно до симплекс-процедури розподілу:
Розв’язок досягається при Використовуючи симплекс-метод, розв’язуємо нову задачу:
Оскільки в рядку, де стоїть від’ємний елемент, немає від’ємних чисел, задача розв’язку не має, допустима область порожня. Це означає те, що при х2≥4 розв’язку даної задачі не існує. Розв’яжемо задачу (13.3), (13.4) за додаткової умови
а) (14.3), (14.4) за умови б) (14.3), (14.4) за умови Розв’язуємо задачу а):
Відповідь: Розв’язуємо задачу б):
Задача знову розпадається на дві: а) (14.3), (14.4), б) (14.3), (14.4), Розв’язуємо задачу а):
Відповідь: Розв’яжемо задачу б):
Аналіз всіх можливих варіантів методу ланцюгів і границь дає можливість зобразити їх наступною схемою (рис. 2).
рис. 2 Завдання для самостійних і контрольних робіт Розв’язати задачі 1-32 у цілих числах або довести, що вони не мають розв’язку.
|

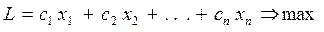 (14.1)
(14.1)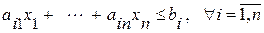 (14.2)
(14.2)
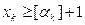 ;
;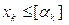 ,
,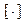 означає цілу частину числа, що в ньому міститься.
означає цілу частину числа, що в ньому міститься.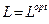 , а змінні, за яких воно досягається, – розв’язок задачі.
, а змінні, за яких воно досягається, – розв’язок задачі.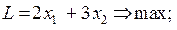 (14.3)
(14.3) (14.4)
(14.4)

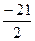
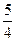




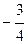
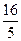

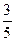



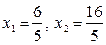 . Будемо виділяти клітинки таблиці з базовим елементом. Оскільки, х1 та х2 не цілі числа, переходимо до виконання п. 2.
. Будемо виділяти клітинки таблиці з базовим елементом. Оскільки, х1 та х2 не цілі числа, переходимо до виконання п. 2.


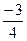

 . Тут і далі значок
. Тут і далі значок  означає цілу частину числа, що стоїть у дужках. Отримаємо:
означає цілу частину числа, що стоїть у дужках. Отримаємо:

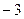
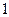


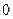

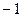



 . Оскільки
. Оскільки  містить дробову частину, то знову розв’язуємо дві задачі:
містить дробову частину, то знову розв’язуємо дві задачі:
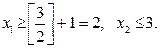
 .
.
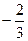
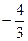
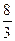




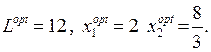 .
.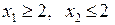
 .
.
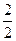

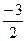
 .
.