Поняття про тензор інерції

Дата добавления: 2014-10-29; просмотров: 1183

Для обертання однорідного тіла навколо осі симетрії зв’язок між векторами і має простий вигляд

або

, , .

Це пояснюється тим, що вектори і колінеарні. Але в загальному випадку вектори і розташовані під певним кутом один до одного і зв’язок між ними більш складний ніж в .

Зв’яжемо аналітично вектори і в загальному випадку. Будемо виходити з того, що модулі і пропорційні один одному. Це випливає з того, що модулі елементарних векторів пропорційні модулю (дивись ), а значить і модуль суми цих векторів також пропорційний модулю .

Легко переконатись, що така пропорційність буде виконуватись тоді, коли кожна із компонент буде залежати лінійно від компонент вектора .

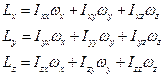
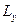Дійсно, при збільшенні в декілька разів, в таку ж кількість разів збільшаться , і , і відповідно кожна із компонент , і 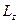, а значить і сам вектор .

Взаємна орієнтація векторів і визначається значеннями коефіцієнтів пропорційності.

Всі три формули можна записати компактно у вигляді одного виразу:

, .

Сукупність дев’яти величин називається тензором другого рангу, а операцію, що виражається формулами називають множенням вектора на тензор . В результаті такого множення одержують вектор .

Тензор прийнято записувати у вигляді таблиці

.

Величини 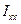, , … називають компонентами тензора інерції. Цей тензор характеризує інертні властивості тіла при обертанні.

Щоб знайти значення компонент тензора інерції будемо виходити із визначення моменту імпульсу тіла:

.

Тут – вектори, відкладені від центра мас тіла (рис.64). Використовуючи кінематичне співвідношення , перепишемо

.

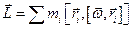Скориставшись формулою „бац мінус цаб” одержимо

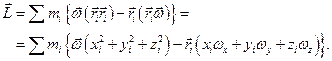
Знайдемо проекцію цього вектора на вісь :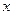

Аналогічно знаходяться проекції вектора на осі і :

,

.

Порівняння знайдених нами виразів з формулами дозволяє знайти значення компонент тензора інерції. Запишемо їх у вигляді таблиці:

.

Діагональні компоненти тензора уявляють собою моменти інерції відносно координатних осей 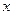, і . Відмітимо, що недіагональні компоненти тензора задовольняють умові , , . Тензор, що задовольняє цим умовам, називається симетричним.

Практично компоненти тензора інерції обчислюються шляхом інтегрування. Наприклад, компонента розраховується за формулою

.

Тут 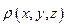– густина, – елементарний об’єм. Інтегрування проводиться по всьому об’єму.

Знайдемо компоненти тензора інерції для однорідного прямокутного паралелепіпеда, вибравши осі координат так, як показано на рис.65. Початок координат співпадає з центром мас тіла .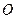

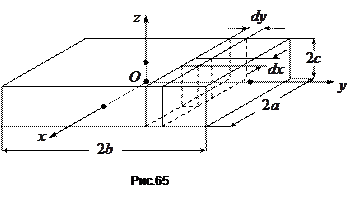
Для обчислення осьового моменту інерції розіб’ємо тіло на стовпчики з площею основи . Об’єм стовпчика дорівнює , а його маса . Тому вклад стовпчика в визначається виразом

.

Проінтегрувавши цей вираз по 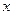, знайдемо вклад в , який дає показаний на рис.65 шар довжиною , шириною і товщиною :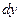

Проінтегрувавши далі цей вираз по , одержимо всього тіла

.

Тут 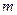– маса сього тіла.

Аналогічні розрахунки приведуть до виразів

, .

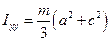Знайдемо один із неосьових моментів, наприклад, . Вклад в цей момент стовпчика з основою дорівнює

,

а вклад шару

.

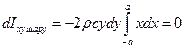Відповідно і весь цей неосьовий момент тіла дорівнює нулю. Таким чином, при даному, показаному на рис.65, виборі координатних осей тензор моменту інерції однорідного прямокутного паралелепіпеда набуває діагонального вигляду, тобто

.

Ми залишили при діагональних компонентах по одному індексу. Величини , , 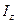називаються головними моментами інерції тіла. Діагональний вигляд тензор інерції має лише в системі координат, зв’язаній з головними осями інерції. Головні осі інерції взаємно-перпендикулярні і пересікаються в центрі мас тіла. В загальному випадку (коли ) ці осі можна вибрати лише одним способом. У симетричної дзиги фіксована лише вісь , дві інші вісі довільні. Для тіла сферичної симетрії вибір головних осей довільний.