Закони Кеплера та закон всесвітнього тяжіння

Дата добавления: 2014-10-29; просмотров: 1907

Закон всесвітнього тяжіння був відкритий Ньютоном в результаті узагальнення дослідних фактів, які встановив Кеплер, спостерігаючи рух планет Сонячної системи. Три закони Кеплера формулюються так.

1. Кожна планета рухається по еліпсу, в одному з фокусів якого знаходиться Сонце.

2. Радіуси-вектори планет описують за однакові проміжки часу однакові площі.

3. Квадрати періодів обертання планет навколо Сонця відносяться як куби великих півосей їх орбіт.

Для спрощення розрахунків, які можна зробити з аналізу цих законів, вважатимемо спочатку, що орбіти планет не еліптичні, а колові. Тоді з перших двох законів Кеплера випливає, що сила, яка діє на планети, напрямлена вздовж радіуса кола, в центрі якого знаходиться Сонце. Для планет Сонячної системи такі наближення близькі до істини.

Прискорення планети 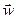, наприклад Землі, при рівномірному русі по коловій орбіті радіуса , яке згідно з другим законом Ньютона виражається формулою

,

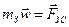запишемо із кінематичного співвідношення

,

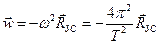де 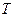– період обертання планети.

Для планет, що рухаються по коловим траєкторіям третій закон Кеплера записується у вигляді

,

або

,

де – стала для всіх планет Сонячної системи. Вона називається сталою Кеплера.

Виключаючи період 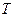в формулі за допомогою рівняння одержуємо

.

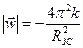Сила, що діє на планету, згідно з рівнянням , за абсолютною величиною дорівнює

.

Ми довели, що сила, з якою Сонце діє на планету, повинна бути обернено пропорційною квадрату відстані планети від Сонця.

Згідно виразу сила , що діє з боку Сонця на Землю, пропорційна масі Землі. Але Сонце і Земля в їх взаємодії виступають як рівноправні партнери. Тому можна сказати, що Земля притягує Сонце з такою ж самою силою, а тому

.

Виходить, що повинна бути пропорційна і , і . Тому для цієї сили взаємодії можна записати

.

Тут – нова стала, так звана універсальна стала всесвітнього тяжіння. Вона одна і та ж сама для всіх тіл. Припустивши, що протягування існує не тільки між Сонцем і планетами, а і між усіма іншими тілами, Ньютон сформулював закон, згідно якому любі два тіла (матеріальні точки) притягуються одне до одного з силами, пропорційними добутку їх гравітаційних мас і обернено пропорційними квадрату відстані між ними.

Підкреслимо, що в приведеному формулюванні закону всесвітнього тяжіння взаємодіючі тіла являються точковими. Це не суперечить рівнянню , яке визначає сили взаємодії між двома кулями, але зовсім не точковими. Вираз для сили взаємодії між двома кулями можна одержати шляхом розрахунку із застосуванням дослідом обгрунтованого принципу суперпозиції гравітаційних полів.

Для перевірки закону всесвітнього тяжіння можна було б поступити так. Припустимо, що Місяць і яблуко притягуються Землею за одним і тим же законом, що визначається формулою з відповідними величинами мас взаємодіючих тіл і відстаней (рис.69). Знаючи прискорення Місяця із відомих параметрів його руху, можна обрахувати прискорення, яке повинно було б мати яблуко

, .

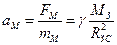Припускаємо, що , тоді

Прискорення місяця можна знайти із виразу

.

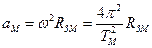Тоді прискорення яблука дорівнює

.

Розраховане прискорення яблука майже співпадає з виміряним .

Константа всесвітнього тяжіння 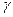вперше була виміряна Г.Кавендішем у 1798 році за допомогою крутильних терезів. Другий метод вимірювання 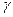здійснювався з використанням терезів за схемою, показаною на рис.70. Робилося два зважування кульки масою 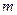, перший раз, коли вона розміщувалася зверху, над кулею 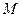, другий – знизу, під кулею .

,

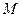, тут .

Віднімаючи від першого друге рівняння одержимо , звідки знаходимо 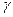. Сучасні виміри дають величину .