
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Рух частинки в полі . Задача Кеплера
Дата добавления: 2014-10-29; просмотров: 1220
|
|
Раніше, розглядаючи рух частинки в центральному полі шляхом розв’язування задачі в полярній системі координат із застосуванням тільки законів збереження енергії і моменту імпульсу, ми прийшли до виразу, яким визначалася б траєкторія руху частинки  . Щоб знайти явну залежність
. Щоб знайти явну залежність  , треба виконати інтегрування в рівнянні
, треба виконати інтегрування в рівнянні
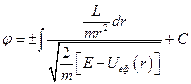
Тут  , де потенціальна енергія взаємодії має вигляд
, де потенціальна енергія взаємодії має вигляд  . Від’ємна величина
. Від’ємна величина 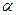 відповідає притягуванню, а додатна – відштовхуванню.
відповідає притягуванню, а додатна – відштовхуванню.
Інтегруємо рівняння
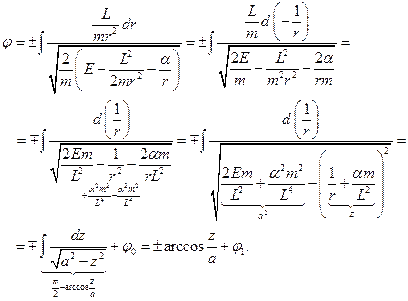
Позначивши  , дістаємо
, дістаємо  або
або
 .
.
 .
.
Тут знак перед одиницею „ 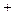 ” відповідає притягуванню
” відповідає притягуванню 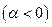 , „
, „  ” відповідає відштовхуванню
” відповідає відштовхуванню 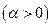 . Позначивши
. Позначивши
 ,
,  ,
,
одержимо рівняння траєкторії частинки
 .
.
Проведемо спочатку якісний аналіз руху частинки.
 1. Відштовхування
1. Відштовхування 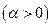
 ,
,  .
.
Оскільки 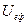 в даному випадку додатна, то як видно із рис.78 маємо тільки інфінітний рух
в даному випадку додатна, то як видно із рис.78 маємо тільки інфінітний рух
2. Притягування 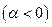

 ,
,  .
.
Як видно із рис.79 можливі такі рухи:
1) при  – фінітний рух, еліпс. Із дослідження кривої
– фінітний рух, еліпс. Із дослідження кривої 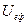 на екстремум одержимо
на екстремум одержимо 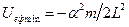 ;
;
2) при  – інфінітний рух, парабола;
– інфінітний рух, парабола;
3) при  маємо інфінітний рух, гіпербола.
маємо інфінітний рух, гіпербола.
Тепер докладніше розглянемо випадок притягування частинки центром 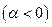 . Траєкторія частинки визначається рівнянням конічного перерізу з фокусом в початку координат.
. Траєкторія частинки визначається рівнянням конічного перерізу з фокусом в початку координат.
 . Тут
. Тут  ,
,  .
.
 – параметр;
– параметр;  – ексцентриситет,
– ексцентриситет, 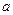 – велика піввісь еліпса,
– велика піввісь еліпса, 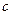 – відстань від фокуса до середини відстані між фокусами.
– відстань від фокуса до середини відстані між фокусами.
| З аналітичної геометрії відомо, що коли | Оскільки  і всі величини під радикалом крім і всі величини під радикалом крім  додатні, то маємо додатні, то маємо
|
 , то траєкторія гіпербола , то траєкторія гіпербола
|  при при 
|
 , то траєкторія парабола , то траєкторія парабола
|  при при 
|
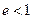 , то траєкторія еліпс , то траєкторія еліпс
| 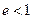 при при 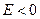
|
 , то траєкторія коло , то траєкторія коло
|  при при 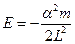
|
Таким чином, розрахунки підтверджують якісні міркування, приведені вгорі (дивись рис.79).
Побудуємо (рис.80) функцію  .
.
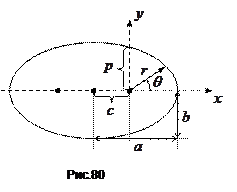 При
При  буде
буде  – перигелій орбіти, найближча точка орбіти до фокуса, центра силового поля.
– перигелій орбіти, найближча точка орбіти до фокуса, центра силового поля.
При  ,
, 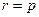 – перетин траєкторією осі
– перетин траєкторією осі  .
.
При 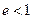 траєкторією буде еліпс, а оскільки
траєкторією буде еліпс, а оскільки  , то це буде при
, то це буде при 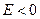 .
.
Ексцентриситет  характеризує витягнутість орбіти. Чим більший
характеризує витягнутість орбіти. Чим більший  , чим ближчий до одиниці, тим орбіта більш витягнута вздовж
, чим ближчий до одиниці, тим орбіта більш витягнута вздовж 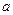 .
.
При  ,
, 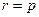 при всіх кутах
при всіх кутах 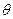 , тобто маємо коло, а це відповідає мінімуму ефективної потенціальної енергії
, тобто маємо коло, а це відповідає мінімуму ефективної потенціальної енергії
 .
.
З аналітичної геометрії відомо, що велика піввісь  . Це співвідношення легко довести:
. Це співвідношення легко довести:  ,
,  .
.  . Мала піввісь
. Мала піввісь  .
.
Підставимо в 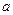 і
і  вирази
вирази  і
і  . Отримаємо
. Отримаємо
 ;
;
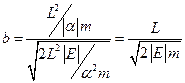 .
.
Як бачимо, велика піввісь залежить тільки від енергії  , мала піввісь залежить крім енергії ще і від моменту імпульсу
, мала піввісь залежить крім енергії ще і від моменту імпульсу  . Величини
. Величини  відмінні від нуля, коли
відмінні від нуля, коли 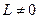 .
.  при
при  , тобто траєкторія вироджується у фінітний рух по прямій, що проходить через силовий центр.
, тобто траєкторія вироджується у фінітний рух по прямій, що проходить через силовий центр.
Видно, що момент імпульсу  визначає опуклість еліпса.
визначає опуклість еліпса.
Визначимо тепер період обертання планети по орбіті. Відомо  . Врахуємо, що
. Врахуємо, що 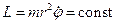 . Тоді
. Тоді  . Інтегруючи цей вираз знайдемо площу за період обертання, тобто площу еліпса, яка, як відомо, дорівнює
. Інтегруючи цей вираз знайдемо площу за період обертання, тобто площу еліпса, яка, як відомо, дорівнює  .
.
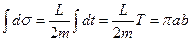
 .
.
Підставляючи вирази 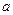 і
і  і в вираз для періоду, будемо відразу знаходити
і в вираз для періоду, будемо відразу знаходити 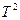
 .
.
Підставляючи  , одержуємо
, одержуємо
 .
.
Тобто видно, що  . Тут
. Тут  – стала Кеплера. Це і є третій закон Кеплера. Отже, закони Кеплера є наслідками законів динаміки та закону всесвітнього тяжіння.
– стала Кеплера. Це і є третій закон Кеплера. Отже, закони Кеплера є наслідками законів динаміки та закону всесвітнього тяжіння.
Побудуємо гіперболу для притягуючого центра 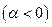

 , а значить
, а значить  .
.

 , тут
, тут  .
.
В даному випадку півосі визначаються так
 ;
; 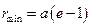
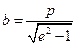 .
.
Ексцентриситет  (дивись на рис.81).
(дивись на рис.81).
Розглянемо відштовхування 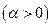 . При цьому можливий тільки випадок
. При цьому можливий тільки випадок  , а значить
, а значить  . Рівняння руху
. Рівняння руху
 .
.
При  ,
,  . Підставимо
. Підставимо  .
.  (рис.82). Тут враховано, що
(рис.82). Тут враховано, що  .
.
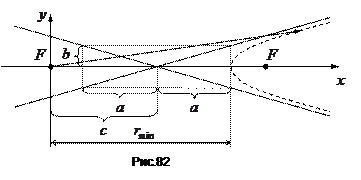
Вигляд траєкторій супутників Землі такий самий як для планет, що рухаються біля Сонця (рис.83).
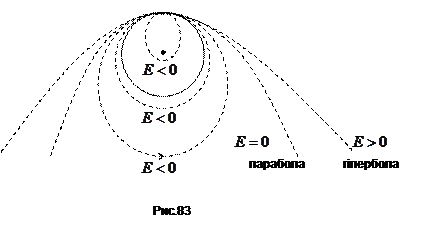
Космічні швидкості:
1) 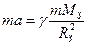 ,
,  ,
, 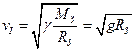
2) повинен бути рух по параболі, тобто  .
.  . Тут нема
. Тут нема 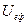 , тому що швидкість не радіальна, а повна
, тому що швидкість не радіальна, а повна 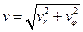 .
. 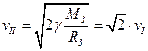 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Застосування законів збереження до опису руху частинки в центральному полі сил | | | Задача двох тіл |