
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Задача двох тіл
Дата добавления: 2014-10-29; просмотров: 1856
|
|
Коли одна маса значно перевищує масу другого тіла, то рух другого тіла описується біля нерухомого масивного тіла – це задача одного тіла.
Коли маси обидві одного порядку, то виникає проблема урахування руху обох тіл – проблема двох тіл.
Розглянемо два тіла  і
і  (рис.84), що взаємодіють по закону всесвітнього тяжіння
(рис.84), що взаємодіють по закону всесвітнього тяжіння

 Тут маємо притягуючий центр
Тут маємо притягуючий центр 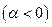 . Як видно з рисунка
. Як видно з рисунка
 .
.
Будемо розв’язувати задачу в системі центра мас (  -системі), помістивши початок координат в центр мас системи. В цьому випадку
-системі), помістивши початок координат в центр мас системи. В цьому випадку
 .
.
Відносна відстань в  -системі та ж сама, що і в лабораторній системі
-системі та ж сама, що і в лабораторній системі
 .
.
Тому з останніх двох рівнянь одержимо
 ,
,  .
.
Застосуємо другий закон Ньютона для кожної із частинок в  -системі
-системі
 ,
,  ;
;
 ,
,  .
.
 .
.
Останнє рівняння можна розглядати як рівняння руху деякої уявної частинки в центральному полі сил. Положення частинки відносно центра сил визначається радіусом-вектором  . Згідно рівнянню уявній частинці слід приписати масу
. Згідно рівнянню уявній частинці слід приписати масу 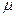 , яка визначається співвідношенням
, яка визначається співвідношенням 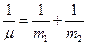 . Звідси
. Звідси 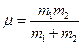 . Величина
. Величина 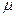 називається зведеною масою частинки.
називається зведеною масою частинки.
Таким чином, задача двох тіл зводиться до задачі про рух одної частинки із зведеною масою 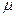 в центральному полі сил. З розв’язку рівняння
в центральному полі сил. З розв’язку рівняння

знаходимо радіус-вектор  як функцію часу. А далі за формулами визначаємо
як функцію часу. А далі за формулами визначаємо 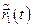 і
і  . Останні вектори відкладаються від центра мас системи. Тому, щоб скористатись формулами , радіус-вектор
. Останні вектори відкладаються від центра мас системи. Тому, щоб скористатись формулами , радіус-вектор  уявної частинки
уявної частинки 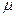 треба теж відкладати від центра мас системи.
треба теж відкладати від центра мас системи.
 Припустимо, в результаті розв’язку одержали траєкторію частинки
Припустимо, в результаті розв’язку одержали траєкторію частинки  , зображену на рис.85. Точка
, зображену на рис.85. Точка 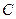 – центр мас системи. Далі будуємо
– центр мас системи. Далі будуємо 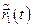 і
і  , які визначаються формулами . На рис.85 побудова здійснена для співвідношення мас
, які визначаються формулами . На рис.85 побудова здійснена для співвідношення мас 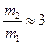 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Рух частинки в полі . Задача Кеплера | | | Малі коливання |