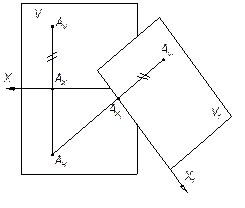Глава 4. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА
Решение позиционных и метрических задач значительно упрощается при преобразовании чертежа так, чтобы заданные геометрические объекты оказались в наиболее удобном – частном положении относительно плоскостей проекций. Это достигается либо способом замены плоскостей проекций, либо способом вращения.
Способ замены плоскостей проекций
Сущность этого способа заключается в том, что рассматриваемый геометрический объект не изменяет своего положения в пространстве, а заменяется одна из плоскостей проекций, при этом соблюдаются следующие условия: новая плоскость должна быть перпендикулярна к оставшейся (незаменяемой) плоскости проекций; положение новой плоскости (новой оси) выбирается в зависимости от условий задачи; линии связи в новой системе проекции перпендикулярны новой оси; расстояния новых проекций от новой оси равны расстояниям от заменяемых проекций до старой оси.
Преобразование чертежа точки и прямой Рассмотрим сущность преобразования чертежа способом замены плоскостей проекций на примере чертежа точки. Пусть в системе плоскостей проекций V / H задана точка А на (рис.4.1).
Рис. 4.1. Преобразование чертежа точки в диметрии
Рис 4.2. Преобразование чертежа точки на эпюре
Заменим плоскость V на V1 перпендикулярную к плоскости Н и под некоторым произвольным углом к плоскости V. Горизонтальная плоскость проекций не меняет своего положения, т.е. осуществляется переход от системы X ( V/H) к новой X1 (V1/H). Плоскость V1 пересекается с плоскостью H по прямой Х1, которая определяет новую ось проекций. Проекция AH остается без изменений, так как точка А и плоскость Н не меняли своего положения в пространстве. Для нахождения новой фронтальной проекции точки AV1, достаточно спроецировать ортогонально точку А на плоскость V1. На рис.4.1 видно, что расстояние новой фронтальной проекции AV1 точки А от новой оси Х1 равно расстоянию от старой фронтальной проекции AV до старой оси Х: | AV AХ | = | AV1 AХ1 |. На рис.4.2 осуществлено совмещение плоскости V1 с H вращением относительно оси X1. Задача: Преобразовать горизонталь АВ во фронтально проецирующую прямую. (рис.4.3).
Рис 4.3. Преобразование чертежа прямой Решение. Новая плоскость V1 перпендикулярна плоскости H и АНВН. Расстояния от точек АV1 и ВV1 до новой оси Х1 на плоскости V1 равно расстоянию от точек АV и ВV до старой оси Х. Задача: Определить натуральную величину и угол наклона отрезка АВ прямой общего положения к плоскости H и V. (рис.4.4а, б).
Рис 4.4. Определение натуральной длины отрезка а) и угла α; б) и угла β Решение. На рис.4.4а выполнена замена фронтальной плоскости проекций V новой плоскостью V1 проекция которой параллельна горизонтальной проекции отрезка АВ, поэтому плоскость V параллельна отрезку. Линии связи перпендикулярны новой оси Х1. От новой оси на линиях связи отложены отрезки, равные расстояниям фронтальных проекций АV и ВV точек до оси Х. В новой системе V1/H отрезок АВ преобразовался во фронталь. На рис.4.4б, показано решение этой же задачи, если отрезок АВ преобразовать в новой системе V/H1 в горизонталь. Задача: Преобразовать прямую общего положения в проецирующую (рис.4.5). Решение. Для того, чтобы прямая общего положения в новой системе плоскостей проекций стала проецирующей, нужно последовательно решить рассмотренные первую и вторую задачи. Первой заменой преобразовать прямую в линию уровня фронталь. Второй заменой фронталь преобразовать в горизонтально-проецирующую прямую.
Рис 4.5. Преобразование чертежа Задача: Определить расстояние между двумя параллельными прямыми k и m (рис.4.6).
Рис 4.6. Определение расстояния между прямыми Решение. Так как m и k фронтали, то заменяем плоскость Н на Н1, причем Н1 берем перпендикулярно прямым m и k, чтобы они стали проецирующими.
|