Ф с прямой АВ с прямой АВ
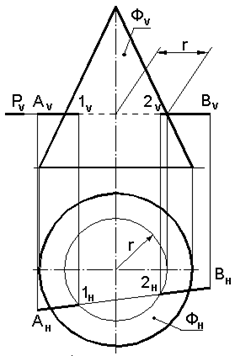
Решение: Решение упрощается, т.к. поверхность цилиндра Ф – горизонтально проецирующая (ось цилиндра перпендикулярна к плоскости Н) и горизонтальная проекция цилиндра – окружность ФН. Следовательно, на горизонтальной плоскости проекций искомые точки определяют непосредственно по линиям связи. Видимость прямой определяют по отношению к поверхности вращения Ф. Задача: Построить точки пересечения конуса с прямой АВ (рис.7.13). Решение: Через прямую АВ проводится вспомогательная PV фронтально-проецирующая плоскость перпендикулярная плоскости V.
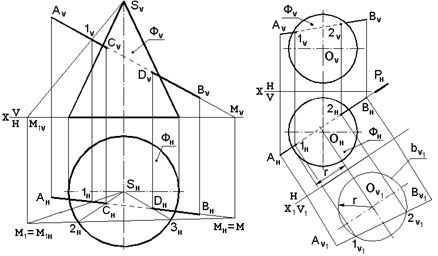
Рис. 7.13. Пересечения конуса с прямой АВ Находится линия пересечения вспомогательной плоскости с поверхностью Ф, которая представляет собой окружность радиусом r. Определяются горизонтальные проекции точек пересечения 1H и 2H прямой АВ и поверхности Ф, как точки пересечения проекции АHВH с окружность радиусом r. По линиям связи находятся точки 1V и 2V на проекции AVBV. Видимость прямой АВ определяется по отношению к поверхности вращения Ф. Часть прямой АВ, заключенная внутри поверхности вращения (между точками 1 и 2), не видна на обеих плоскостях проекций. На горизонтальной плоскости проекций точки 1 и 2 видимы, т. к. они находятся над основанием поверхности вращения Ф. На фронтальной плоскости проекций точки 1 и 2 также являютсявидимыми, так как они располагаются перед фронтальным меридианом. Задача: Построить, точки пересечения конуса Ф с прямой АВ общего положения (рис.7.14). Решение: Для решения задачи в качестве вспомогательной рационально применить плоскость общего положения Р, проходящую через прямую АВ и вершину конуса S. Плоскость зададим двумя пересекающимися прямыми АВ и S1. Точка 1 берется произвольно на прямой АВ.
Рис.7.14. Пересечение конуса Рис.7.15. Пересечение сферы
|