Конус. Возможные сечения

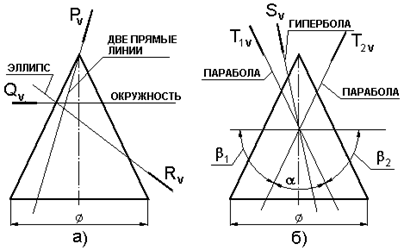
Если секущая плоскость проходит через вершину конуса (i, l), то онапересекает его по двум образующим (рис.7.5а, плоскость Р).

Если же конус пересекает плоскость, не проходящая через его вершину, то в сечении получится одна из следующих кривых:

· окружность, если секущая плоскость перпендикулярна к его оси (рис.7.5а, плоскость Q);

· эллипс, если секущая плоскость пересекает все образующие одной плоскости конуса и не перпендикулярна к его оси (рис.7.5а, плоскость R);

· парабола, если секущая плоскость параллельна одной из образующих конуса (рис.7.5б, плоскости Т₁ и Т₂). В этом случае угол между секущей плоскостью и осью конуса равен углу между осью конуса и образующей;

Рис. 7.5. Сечения конической поверхности вращения

 

 

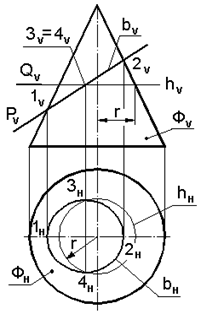
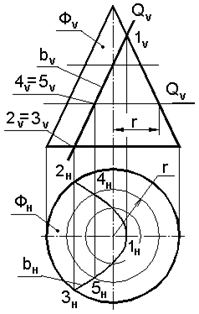
· гипербола, если секущая плоскость параллельна двум образующим конуса (рис.7.5б, плоскость S). При этом угол между секущей плоскостью и осью конуса меньше угла между осью конуса и образующей.

Следует обратить внимание на углы a, b₁, b₂ (рис.7.5б).

Угол a - между следами T_1V и T_2V плоскостей, пересекающих конус по параболам. Если проводить следы плоскостей через точку О внутри угла a, то эти плоскости пересекут конус по гиперболам, а если внутри углов b₁ и b₂, то по эллипсам.

Задача: Построить линию пересечения конуса, поверхность Ф, с фронтально проецирующей плоскостью Р (рис.7.6).

Решение:

Линия пересечения b – эллипс (см. рис.7.5, плоскость R).

[1 2] – большая ось эллипса.

[3 4] – малая ось эллипса.

[1 2] – натуральная величинабольшой оси эллипса.

Точки 3_V и 4_V делят большую ось эллипса пополам.

Если через эти точки провести окружность – параллель h, то натуральная величина малой оси определится как хорда [3_Н4_Н] горизонтальной проекции окружности – параллели h_Н.

Ряд произвольных точек строят при помощи окружностей – параллелей.

Задача: Построить линию пересечения конуса, поверхность Ф, фронтально проецирующей плоскостью Q (рис.7.7).

Решение:

Линия пересечения b – парабола (см. рис.7.5, плоскости Т₁ и Т₂)

1 – вершина параболы,

S_H – фокуспараболы (вершина конуса),

2 и 3 – точки, ограничивающие параболу.

Ряд произвольных точек строят при помощи окружностей – параллелей h_v так, как это показано для точек 4 и 5.

Рис. 7.6. Сечение конической Рис. 7.7. Сечение конической