К) внутри тороида на произвольном расстоянии r от его центра
B = mm0nIR/r; H = nIR/r, (5.27) где l = 2pr - длина оси тороида; R – радиус тороида по средней линии; r - радиус тороидального кольца; I - сила тока; N - число витков тороида; n - число витков на единицу длины тороида. Циркуляция вектора индукции магнитного поля по замкнутому контуру L (или просто циркуляцией вектора индукции магнитного поля) – физическая величина, определяемая линейным интегралом:
где d l – вектор элементарной длины замкнутого контура, направленной вдоль обхода контура; Bl = B× cosa - составляющая вектора B в направлении касательной к контуру (с учетом выбранного направления обхода); a - угол между векторами B и d l. Циркуляция вектора напряженности магнитного поля по замкнутому контуру L (или просто циркуляция вектора напряженности магнитного поля) - физическая величина, определяемая линейным интегралом:
где d l – вектор элементарной длины замкнутого контура, направленной вдоль обхода контура; Hl = H× cosa - составляющая вектора H в направлении касательной к контуру (с учетом выбранного направления обхода); a - угол между векторами H и d l. Закон полного тока (теорема о циркуляции индукции магнитного поля) в интегральной форме: циркуляция вектора индукции магнитного поля по замкнутому контуру L равна произведению mm0 на алгебраическую сумму токов, охватываемых контуром (направление обхода контура и направление тока должны быть связаны между собой правилом правого винта):
где n – число проводников с токами, охватываемых контуром L произвольной формы. Следствия из закона полного тока: 1) если направление обхода контура и направление тока в проводнике не связаны между собой правилом правого винта, то значение циркуляции вектора магнитной индукции, сохранив величину, изменит знак; 2) если контур, расположенный в магнитном поле, не охватывает ток или алгебраическая сумма токов внутри замкнутого контура равна нулю:
Закон полного тока (теорема о циркуляции индукции магнитного поля) в дифференциальной форме справедлив для произвольных токов и контуров: rot B =mm0 j. 5.32 Условие непотенциальности магнитного поля (вихревого характера магнитного поля):
Поток магнитной индукции (магнитный поток) через площадку dS - физическая величина, численно равная произведению проекции B на направление положительной нормали n и величины этой площадки dS: dФm=Bn× dS=B× dS× cosa, (5.34) где a - угол между векторами Bиn; Bn = B× cosa - проекция вектора B на направление положительной нормали к площадке dS. Полный поток магнитной индукции через некоторую поверхность S
Для однородного магнитного поля и плоской площадки S Фm = Bn× S. (5.36) Теорема Остроградского-Гаусса для магнитных полей:
Индукция магнитного поля B в магнитной цепи, состоящей из стального сердечника с воздушным (вакуумным) зазором:
где lc, lВ - соответственно длина стального и воздушного участков цепи; mс, mВ - их магнитные проницаемости; I - ток в обмотке цепи; N - число витков обмотки. Закон Ома для магнитных цепей:
где I× N = Eм - магнитодвижущая сила; Rмс = Rмв = Rм = Rмс + Rмв - полное сопротивление магнитной цепи. Законы (правила) Кирхгофа для магнитных цепей: 1. Первый: Алгебраическая сумма магнитных потоков в участках цепи, сходящихся в узле, равна нулю:
Примечание: знак Фмi определяется направлением соответствующих линий B. Если линии вектора B сходятся в узле, Фмi - положителен, если они выходят из узла, Фмi - отрицателен. 2. Второй: В любом замкнутом магнитном контуре, произвольно выбранном в разветвленной магнитной цепи, алгебраическая сумма произведений магнитных потоков на магнитное сопротивление соответствующих участков цепи равна алгебраической сумме магнитодвижущих сил этого контура:
При последовательном соединении магнитопроводов полное магнитное сопротивление равно сумме магнитных сопротивлений отдельных последовательно соединенных участков: Rм = При параллельном соединении величина, обратная сопротивлению разветвленной части магнитной цепи, равна сумме обратных величин магнитных сопротивлений отдельных ветвей:
5.2. Силы, действующие на ток в электромагнитном поле Сила, действующая в магнитном поле на элемент объема тела dV: d F =e [ v ´ B ]∙ dN = n∙ e∙ [ v ´ B ]dV = [ j ´ B ]dV, (5.43) где e- величина заряда электрона; n - концентрация свободных электронов; dN = n∙ dV - число заряженных частиц в объеме dV; j= nev - плотность тока; v - скорость направленного движения свободных электронов; B - индукция магнитного поля. Сила (сила Ампера), действующая на проводник с током в магнитном поле (закон Ампера):
|

 , (5.28)
, (5.28) , (5.29)
, (5.29)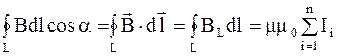 , (5.30)
, (5.30)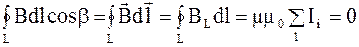 . (5.31)
. (5.31)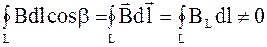 . (5.33)
. (5.33)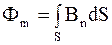 . (5.35)
. (5.35)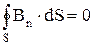 . (5.37)
. (5.37)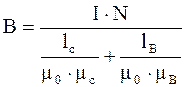 , (5.38)
, (5.38)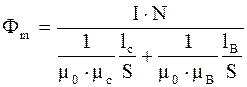
 , (5.38)
, (5.38) - магнитное сопротивление цепи сердечника;
- магнитное сопротивление цепи сердечника; - магнитное сопротивление цепи воздушного зазора;
- магнитное сопротивление цепи воздушного зазора; . (5.39)
. (5.39) . (5.40)
. (5.40)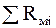 . (5.41)
. (5.41) . (5.42)
. (5.42)


