Расчет статической прочности вала

 

Из рис. 13 следует, что опасными сечениями для рассматриваемого вала, которые необходимо проверить на прочность, являются сечения: (z = 0 ), как наименее жесткое при кручении d_в1 = 26, 5 мм, а также сечения (z = a) и (z = a + b), где действуют наибольшие изгибающие моменты.

В сечении (z = 0)находится еще и шпоночный паз, ослабляющий его жесткость. Сечение (z = a), где; действует изгибающий момент

.

и крутящий момент M_z = 104, 17 Н ∙ м, находится в сложном напряженном состоянии и при этом имеет диаметр, незначительно превышающий наименьший. В сечении (z = a + b) изгибающий момент достигает наибольшей величины

.

Рассчитаем наибольшие напряжения в опасных сечениях.

В сечении (z = 0) нормальные напряжения от осевых сил и изгибающих моментов равны нулю, касательные напряжения τ _max определяются крутящим моментом М_z = 104, 17 H ∙ м и полярным моментом сопротивления сечения W_p цилиндрического конца вала со шпоночным пазом, глубиной t = 5 мм (см. табл. 8).

.

Тогда наибольшие касательные напряжения:

,

а условие прочности вала в сечении (z = 0)

выполняется.

В сечении (z = a) наибольшие нормальные напряжения определяются величиной изгибающего момента М_а = 183, 8 Н ∙ м и моментом сопротивления сечения вала

о наибольшие касательные напряжения этого сечения с полярным моментом , равны

.

В качестве допустимых напряжений на изгиб примем

.

При этом условие статической прочности по приведенным напряжениям,

, выполняется.

В сечении (z = a + b)рассчитаем аналогично, с учетом того, что наибольшие нормальные напряжения определяются величиной изгибающего момента и моментом сопротивления сечения вала (с диаметром шестерни по впадинам):

Условие статистической прочности по приведенным напряжениям,

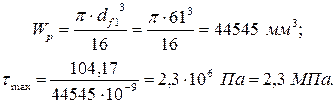
, выполняется.