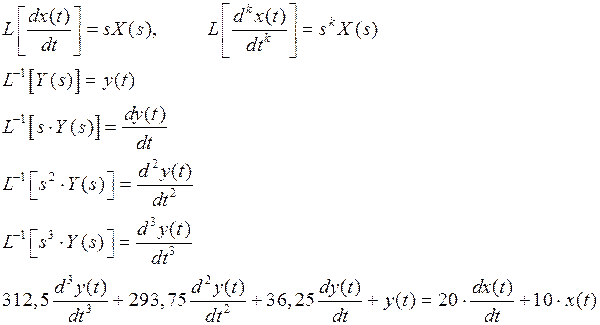Передаточная функция систем управленияТеперь применим преобразование Лапласа к анализу систем управления. Дифференциальное уравнение линейной системы управления в общем виде может быть представлена:
Умножая все слагаемые дифференциального уравнения (2.41) на множитель е -st и производя интегрирование по переменной времени, т.е. подвергая левую и правую части равенства преобразованию Лапласа, получаем
Применяя к этой зависимости правило дифференцирования оригиналов (см. формулу 2.29 и 2.30) при нулевых начальных условиях и свойство линейности, находим уравнение динамики системы в операторной форме:
Введем обозначение для дроби, полученной по свойству пропорции:
Функцию, представляющую собой отношение изображения выходного сигнала Y (s) к изображению входного сигнала X (s) при нулевых начальных условиях, называют передаточной функцией системы W (s). Знаменатель передаточной функции W (s) называется характеристическим многочленом (полиномом) или собственным оператором
а уравнение
Корни характеристического уравнения называются полюсами системы, корни числителя передаточной функции - нулями системы.
Пример: По передаточной функции системы управления W (s) записать дифференциальное уравнение (уравнение динамики) функционирования системы управления при нулевых начальных условиях
Преобразуем передаточную функцию, перемножив скобки:
После раскрытия скобок получается уравнение динамики системы в операторной форме
Взяв обратное преобразование Лапласа от левой и правой частей уравнения и применив свойство линейности преобразования Лапласа, получаем
Полученное уравнение и является искомым дифференциальным уравнением (уравнением динамики) функционирования системы управления при нулевых начальных условиях.
|
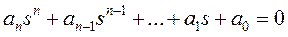- характеристическим уравнением.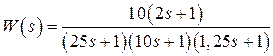
.
Далее применяется свойство дифференцирования оригинала при нулевых начальных условиях:
