Весовая функция (функция веса)
Весовая функция w(t) – реакция системы на краткосрочный импульс δ (t)-дельта-функцию, которая обладает следующими свойствами:
Так как изображение Лапласа от входного импульсного воздействия
Подставляя сюда значение функции H (s), имеем:
Т.к.
Пример Используя таблицу обратного преобразования Лапласа, найти весовую функцию w (t) системы с передаточной функцией W (s) (оригинал w (t) функции по известному изображению W (s)):
Для удобства пользования таблицей преобразования Лапласа найдем корни характеристического уравнения
Решая систему алгебраических уравнений, полученную из равенства дробей (при равенстве знаменателей, равны и числители дробей)
Используя свойство линейности преобразования Лапласа (2.25), находим оригиналы по каждому из слагаемых в отдельности (табл.2.1) и получаем результат временную весовую функцию системы Применяя известную зависимость между переходной характеристикой и весовой функцией
|
то
.
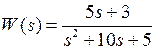и разложимзнаменатель дроби на два сомножителя первого порядка.
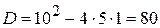
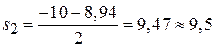
получаем 
, 
.
.
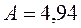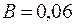, определяется переходная характеристика.
