Оператор polyroots отыскивает корни характеристического уравнения (полюсы системы), очевидно, что они являются левыми, т.е. система устойчивая
Критерий устойчивости Гурвица Для оценки устойчивости с использованием алгебраического критерия Гурвица используются коэффициенты a i характеристического многочлена системы A (s)
При этом составляется определитель Гурвица и его диагональные миноры
который должен быть положительным Так как для системы второго порядка характеристический многочлен
то определитель имеет вид
условиями устойчивости здесь будут: Характеристический многочлен системы третьего порядка будет иметь вид
Определитель Гурвица для нее
Отсюда следует, что кроме выполнения условий
Пример Оценить устойчивость системы управления, передаточная функция которой
Характеристический многочлен системы
поэтому определитель Гурвица
Вычисляя миноры определителя, получаем
Отсюда следует, что рассматриваемая система не устойчива.
|
.
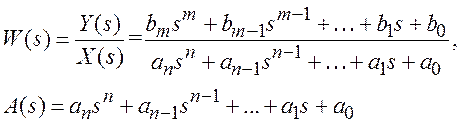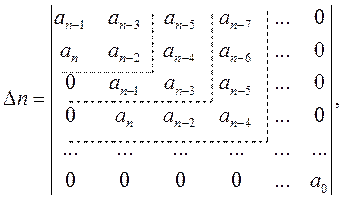
как и все его диагональные миноры: 
, 
.
,
,
, 
и 
.
.
.
необходимо также выполнить условие
.
.
,
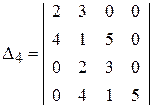
