Шашырандының түрлері және қосу ережесі
Статистикада біртнктес ө згерме кө рсеткіштерінің бір немесе бірнеше топтарғ а бө лінуіне байланысты шашыранды да ү ш тү рге бө лінеді: жалпы, топаралық жә не топтық немесе топішілік. Жалпы шашыранды (σ 2 ) – жалпы ө згермелі жиынтық белгілеріне ә серін тигізетін барлық жағ дайлар мен себептерді сипаттайды жә не мына формула бойынша есептеледі:
Топаралық шашыранды (σ 2 ) – деп жеке топтық орташа шаманың жалпы жиынтық ты орташа ауытқ уын айтады жә не ол мына формула бойынша есептеледі:
Мұ нда,
n-топтардың саны
i- Рет саны 1, 2, 3,...т.б. Топаралық шашыранды ө згерме белгілеріне ә серін тигізетін тұ рақ ты себептерді кө рсетеді. Мұ нда топтау негізінде ә серін тигізетін тұ рақ ты себептердің ө згергендігі қ арастырылады. Яғ ни, жалпы жиынтық тың ө зіне тә н ө згермелі белгілері бойынша жеке топтарғ а бө лінуін анық тайды. Топтық (топішілік) шашыранды немесе орташа топтық шашыранды ( Орташа топтық шашыоандыны топтау негізіндегі себептерден бө лек басқ а себептердің ә сер етуінен кездейсоқ ө згергендігі кө рсетіледі. Оны есептеу ү шін алдымен ә рбір топ бойынша топтық шашыранды ( Онда орташа топтық шашыранды мына формула бойынша есептелінеді:
Мұ нда,
i- рет саны 1, 2, 3...т.б.
Математикалық статистикада жалры шашыранды σ 2 ә рқ ашанда топаралық шашыранды(δ 2 ) мен орташа топтық шашыранды шамаларының қ осындысына тең болады. Жә не кө рсетіледі:
Мұ ны шашыранды қ осындысының ережесі деп те атайды. Бұ л ереженің ө зіне тә н ілімдік жә не тә жіриебелік маң ызы мынады: біріншіден, егер жоғ арыда берілген тең дестіктің екі шамасы белгілі болса, онда белгісіз шаманы анық тауғ а немесе есептелген кө рсеткіштердің дұ рыстығ ын тексеруге болады:
Екіншіден, бұ л ереженің маң ызды болып саналатыны сонда, егер жалпы шашыранды мен топаралық шашыранды есептелген болса, онда топтау белгісінің ә серін тез анық тай аламыз. Ү шіншіден, топтық шашыранды жалпы шашырандыдан ә рдайым кіші болады Егер топаралық шашырандыны жалпы шашырандығ а бө летін болсақ, онда одан шық қ ан кө рсеткішті тө мендеу (детерминация) коэффициенті деп атайды. Статистикада оны гректің η 2 (эта) – ә рпімен белгілейді жә не тө менде берілген формула арқ ылы есептеледі.
Егер осы берілген формуланы шаршы тү бірге алатын болсақ, онда корреляциялық қ атыстылық анық талады
|

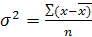 жай тү рі,
жай тү рі, салмақ талғ ан тү рі.
салмақ талғ ан тү рі. жай тү рі,
жай тү рі, 

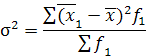 салмақ талғ ан тү рі.
салмақ талғ ан тү рі. - ә р топтың орташа шамасы
- ә р топтың орташа шамасы - жалпы жинақ тың орташа шамасы
- жалпы жинақ тың орташа шамасы - ә р топтың жиілігі
- ә р топтың жиілігі жә не
жә не  ) деп ә рбір топ бойынша кездейсоқ себетердің тигізген ә серінен оның ө згергендігін жә не мә ні мен маң ызын анық тауды айтады.
) деп ә рбір топ бойынша кездейсоқ себетердің тигізген ә серінен оның ө згергендігін жә не мә ні мен маң ызын анық тауды айтады.
 - топтық (топішілік) шашыранды
- топтық (топішілік) шашыранды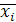 - орташа топтық шама
- орташа топтық шама - ә р топтың жиілігі
- ә р топтың жиілігі
 немесе
немесе 
 σ 2. Себебі, жеке жиынтық бірліктері жалпы жиынтық бірліктерімен салыстырғ анда біртекті болып келеді.
σ 2. Себебі, жеке жиынтық бірліктері жалпы жиынтық бірліктерімен салыстырғ анда біртекті болып келеді.
 ) жә не топтық пен қ орытындылаушы белгілердің арасындағ ы тағ ыз байланысты байқ ауғ а мү мкіндік туады, яғ ни топтық белгілердің қ орытындылаушы белгілерге ә серін тигізуін сипаттайды.[30]
) жә не топтық пен қ орытындылаушы белгілердің арасындағ ы тағ ыз байланысты байқ ауғ а мү мкіндік туады, яғ ни топтық белгілердің қ орытындылаушы белгілерге ә серін тигізуін сипаттайды.[30]


