Отношения эквивалентности
Рассмотрим три отношения: M, S, H. Отношение М описано в 1.2.4. Отношение S введем на множестве X всех треугольников следующим образом: этому отношению принадлежат пары треугольников такие, что площадь треугольника x равна площади треугольника y. Отношение Н действует на множестве жителей г. Томска и содержит пары Свойства этих трех отношений приведены в таблице 1.3, где Р означает рефлексивность, АР – антирефлексивность, С – симметричность, АС - антисимметричность, НС – несимметричность, Т – транзитивность отношения. В качестве упражнения проверьте правильность заполнения таблицы, пользуясь определениями свойств бинарных отношений.
Таблица 1.3 Свойства отношений
Мы видим, что отношения обладают одинаковыми свойствами, поэтому их относят к одному типу. Определение. Отношение R на множестве Х называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности, транзитивности. Таким образом, отношения M, S, H являются отношениями эквивалентности на соответствующих множествах Х. Важной особенностью отношений эквивалентности является то, что они разбивают все множество Х на непересекающиеся подмножества – классы эквивалентности. Определение. Классом эквивалентности, порожденным элементом Так, отношение М разбивает множество Классы эквивалентности образуют систему непустых непересекающихся подмножеств множества Х, в объединении дающую все множество Х – т.е. образуют разбиение множества Х (см. 1.1.6). Отношение эквивалентности обозначают “ º “, поэтому определение класса эквивалентности можно записать так: Множество различных классов эквивалентности множества X по отношению R называется фактор-множеством и обозначается
Теорема 1. Пусть R – отношение эквивалентности на множестве X и Доказательство. По условию теоремы R – отношение эквивалентности, т.е. рефлексивно, симметрично и транзитивно. Покажем, что а) б) в) Условие а выполняется по определению класса эквивалентности и по свойству рефлексивности, т.к. Условие б выполняется, так как каждый элемент множества X попадает в какой-либо класс эквивалентности и Условие в докажем методом “от противного”. Пусть Действительно, возьмем произвольный элемент
Условие в доказано: если классы эквивалентности не совпадают, то они не пересекаются. Следовательно, фактор-множество Теорема 2. Всякое разбиение множества X порождает на X отношение эквивалентности. Доказательство. Пусть Покажем, что R – отношение эквивалентности. Рефлексивность отношения R следует из условия Покажем, что отношение R симметрично. Пусть
Покажем, что R транзитивно. Пусть Отношение R обладает свойствами рефлексивности, симметричности, транзитивности, т.е. является отношением эквивалентности. Теорема доказана.
|

 такие, что х и у носят шляпы одинакового размера.
такие, что х и у носят шляпы одинакового размера. , называется подмножество
, называется подмножество  множества Х, для элементов которого выполняется условие
множества Х, для элементов которого выполняется условие  . Таким образом, класс эквивалентности
. Таким образом, класс эквивалентности 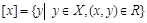 .
.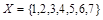 на три класса эквивалентности:
на три класса эквивалентности:  . Класс, порожденный элементом 4, совпадает с классом [1]; [5] = [2], [3] = [6], [7] = [1].
. Класс, порожденный элементом 4, совпадает с классом [1]; [5] = [2], [3] = [6], [7] = [1].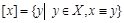 .
.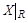 . Так, для отношения M фактор-множество состоит из трех элементов:
. Так, для отношения M фактор-множество состоит из трех элементов: .
.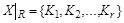 - разбиение множества X, т.е.
- разбиение множества X, т.е. Æ;
Æ; ;
;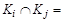 Æ,
Æ,  .
. для любого
для любого  .
.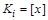 и
и  - разные классы эквивалентности (т.е.
- разные классы эквивалентности (т.е.  и
и  отличаются хотя бы одним элементом). Покажем, что они не пересекаются. Предположим противное: найдется элемент
отличаются хотя бы одним элементом). Покажем, что они не пересекаются. Предположим противное: найдется элемент  такой, что
такой, что  и
и 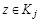 . По определению класса эквивалентности
. По определению класса эквивалентности  и
и  . По свойствам симметричности и транзитивности отношения R имеем:
. По свойствам симметричности и транзитивности отношения R имеем: 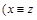 и
и  - отсюда следует равенство множеств
- отсюда следует равенство множеств 
 в силу произвольности a следует
в силу произвольности a следует  . Возьмем произвольный элемент
. Возьмем произвольный элемент  :
:  - в силу произвольности b следует
- в силу произвольности b следует 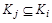 . По определению равенства множеств
. По определению равенства множеств  .
.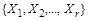 - разбиение множества X. Рассмотрим на X отношение
- разбиение множества X. Рассмотрим на X отношение 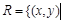 найдется
найдется 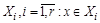 и
и 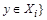 .
.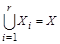 . Каждый элемент множества X попадает в одно из множеств
. Каждый элемент множества X попадает в одно из множеств  , поэтому
, поэтому  .
. . Это означает, что
. Это означает, что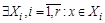 и
и 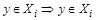 и
и 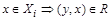 .
. . Тогда найдется множество
. Тогда найдется множество  и
и 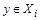 и множество
и множество  и
и 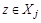 . Но так как различные блоки разбиения не пересекаются, а
. Но так как различные блоки разбиения не пересекаются, а 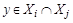 , то
, то 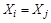 . Следовательно,
. Следовательно,  и R транзитивно.
и R транзитивно.


