Декартовым произведением  двух множеств X и Y называется множество всех упорядоченных пар (x, y)таких, что
двух множеств X и Y называется множество всех упорядоченных пар (x, y)таких, что  , а
, а  .
.
Пример 1. Пусть  . Тогда
. Тогда
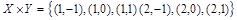 ,
,
 .
.
Очевидно, что  , т.е. для операции декартова произведения множеств закон коммутативности не выполняется.
, т.е. для операции декартова произведения множеств закон коммутативности не выполняется.
Декартовым произведением множеств  будем называть множество
будем называть множество  всех упорядоченных наборов
всех упорядоченных наборов 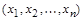 таких, что
таких, что  Если
Если 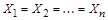 , то декартово произведение обозначают
, то декартово произведение обозначают 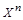 .
.
Будем говорить, что задано соответствие q между множествами X и Y, если задана упорядоченная тройка  , где
, где  . Множество X называется областью отправления, а Y – областью прибытия соответствия q (обозначают
. Множество X называется областью отправления, а Y – областью прибытия соответствия q (обозначают  ). Каждый элемент y в паре
). Каждый элемент y в паре 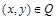 называется образом элемента x (x – прообразом элемента y) при данном соответствии q.
называется образом элемента x (x – прообразом элемента y) при данном соответствии q.
Соответствие  называется отображением множества X во множество Y, если каждый элемент
называется отображением множества X во множество Y, если каждый элемент  имеет образ
имеет образ 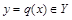 , т.е.
, т.е.
 .
.
Отображение  называется функциональным, если каждый элемент
называется функциональным, если каждый элемент  имеет единственный образ
имеет единственный образ 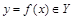 :
:
 .
.
Множество образов при данном отображении  обозначается
обозначается  :
:
 .
.
Если множество  совпадает с множеством Y, то говорят, что
совпадает с множеством Y, то говорят, что  осуществляет отображение на множество Y.
осуществляет отображение на множество Y.
Соответствие  называется взаимно однозначным (биекцией), если
называется взаимно однозначным (биекцией), если
а) является отображением;
б) функционально;
в) отображает X “на” множество Y;
г) из условия  следует
следует  .
.
Другими словами,  является биекцией, если каждый элемент
является биекцией, если каждый элемент  имеет единственный образ
имеет единственный образ 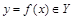 , а каждый элемент
, а каждый элемент  имеет единственный прообраз
имеет единственный прообраз  при данном отображении:
при данном отображении:
 (1.2)
(1.2)

 двух множеств X и Y называется множество всех упорядоченных пар (x, y)таких, что
двух множеств X и Y называется множество всех упорядоченных пар (x, y)таких, что  , а
, а  .
. . Тогда
. Тогда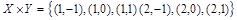 ,
, .
. , т.е. для операции декартова произведения множеств закон коммутативности не выполняется.
, т.е. для операции декартова произведения множеств закон коммутативности не выполняется. будем называть множество
будем называть множество  всех упорядоченных наборов
всех упорядоченных наборов 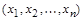 таких, что
таких, что  Если
Если 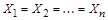 , то декартово произведение обозначают
, то декартово произведение обозначают 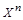 .
. , где
, где  . Множество X называется областью отправления, а Y – областью прибытия соответствия q (обозначают
. Множество X называется областью отправления, а Y – областью прибытия соответствия q (обозначают  ). Каждый элемент y в паре
). Каждый элемент y в паре 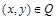 называется образом элемента x (x – прообразом элемента y) при данном соответствии q.
называется образом элемента x (x – прообразом элемента y) при данном соответствии q.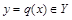 , т.е.
, т.е. .
. называется функциональным, если каждый элемент
называется функциональным, если каждый элемент 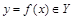 :
: .
. :
: .
. совпадает с множеством Y, то говорят, что
совпадает с множеством Y, то говорят, что  следует
следует  .
. при данном отображении:
при данном отображении: (1.2)
(1.2)


