Системы множеств
Элементы множества сами могут быть множествами: Булеаном B (Х) множества Х называется множество всех подмножеств множества Х. Например, для множества Разбиением R (Х) множества Х называется система его непустых непересекающихся подмножеств, в объединении дающая множество Х (рис. 1.4).
U X X1 X2
X3 X4
Рис. 1.4. Разбиение множества R Например, для множества Покрытием P (X) множества X называется система его непустых подмножеств, в объединении дающая множество X (рис. 1.5).
В этом определении отсутствует слово “непересекающаяся” – т.е. блоки могут иметь общие элементы. Пример. Для множества 1.1.7. Законы алгебры множеств
Так же, как операции обычной алгебры, операции над множествами выполняются по законам (табл. 1.1), которые доказываются на основе введенных выше определений. Особенностью алгебры множеств является закон идемпотентности, благодаря которому в алгебре множеств нет числовых коэффициентов и степеней. Таблица 1.1 Законы алгебры множеств
Докажем закон дистрибутивности А È (В Ç С)= (А È В) Ç (А È С). (1.1) Обозначим X левую часть равенства (1.1), Y – правую. Согласно определению равенства множеств покажем, что выполняются одновременно Пусть x – произвольная точка из множества X=А È (В Ç С). Тогда по определению объединения множеств (
Таким образом для любого Докажем теперь, что
В силу произвольности Таким образом,
|

 ; в таком случае удобно говорить о системе множеств. Рассмотрим такие системы множеств, как булеан, разбиение и покрытие множеств.
; в таком случае удобно говорить о системе множеств. Рассмотрим такие системы множеств, как булеан, разбиение и покрытие множеств. булеаном является множество B
булеаном является множество B  Æ,
Æ,  .
. 





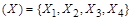
 можно построить разбиение R1
можно построить разбиение R1  , состоящее из двух элементов (они называются блоками разбиения), или разбиение R2
, состоящее из двух элементов (они называются блоками разбиения), или разбиение R2 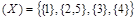 – из четырех блоков; возможны и другие разбиения этого множества Х.
– из четырех блоков; возможны и другие разбиения этого множества Х.
 покрытиями являются системы множеств
покрытиями являются системы множеств  и
и  .
. =Æ
=Æ
 = А
= А

 и
и  .
.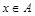 или
или 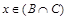 ). Далее по определению пересечения множеств (
). Далее по определению пересечения множеств ( и
и 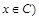 ). Следовательно,
). Следовательно, или
или  и (
и ( и
и 

 выполняется
выполняется  , т.е.
, т.е.  . Тогда
. Тогда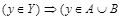 и
и  или
или  и
и 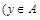 или
или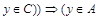 или
или  и
и 
 .
. заключаем
заключаем  , и закон дистрибутивности доказан.
, и закон дистрибутивности доказан.


