Основные определения. Пустым множеством называется множество Æ, не содержащее ни одного элемента, т.е
Множества и операции над ними
Пустым множеством называется множество Æ;, не содержащее ни одного элемента, т.е. для любого элемента x выполняется Универсальным называется множество U всех элементов, рассматриваемых в данной задаче. Пример. Пусть U = Z и требуется найти все решения уравнения Пусть теперь U = R. Тогда множество М решений уравнения Будем говорить, что множество А включается во множество В 1) 2) Если 3) Æ 4) Подмножество Определим понятие равенства множеств: А=В тогда и только тогда, когда одновременно выполняются два включения
Свойства равенства множеств: 1) для любого А справедливо А=A; 2) если А=В, то и В=A; 3) если А=В и В=C, то A=C.
1.1.4. Диаграммы Эйлера – Венна
Эти диаграммы применяются для наглядного изображения множеств и их взаимного расположения.
U
A B
Рис. 1.1 Диаграмма Эйлера-Венна Универсальное множество U изображается в виде прямоугольника, а произвольные множества – подмножества универсального – в виде кругов (рис. 1.1). При этом возможны следующие случаи взаимного расположения двух множеств А и В: 1) одно из множеств строго включается в другое ( 2) множества равны; 3) множества не имеют общих элементов; 4) множества находятся в общем положении, т.е. не подходит ни один из вышеперечисленных случаев, и множества расположены как на рис. 1.1.
|

 Æ;.
Æ;. . Множество М решений этой задачи есть пустое множество: М = Æ.
. Множество М решений этой задачи есть пустое множество: М = Æ. .
. , если каждый элемент множества А является элементом множества В (говорят также, что А является подмножеством множества В). Из определения включения следуют свойства:
, если каждый элемент множества А является элементом множества В (говорят также, что А является подмножеством множества В). Из определения включения следуют свойства: для любого множества А;
для любого множества А;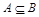 и
и 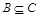 , то
, то  ;
;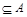 для любого множества А;
для любого множества А; U для любого множества А.
U для любого множества А. - строгое включение), если А не пусто и не совпадает с В. Например, имеют место строгие включения: N
- строгое включение), если А не пусто и не совпадает с В. Например, имеют место строгие включения: N  Z
Z  , т.е. каждый элемент множества А является элементом множества В и каждый элемент множества В является элементом множества А:
, т.е. каждый элемент множества А является элементом множества В и каждый элемент множества В является элементом множества А:

 );
);


