Решающие функции
Теория решающих функций является одной из наиболее новых областей статистики. Хотя они применяются широко, решающие функции здесь представлены только на примере контроля качества товара. Очевидно, что в некотором объеме товара процент брака оценивается тем точнее, чем больше элементов выбирается для пробы. Снятие пробы со многими элементами, однако, может быть связано с большими расходами. Может быть дорогостоящим и исследование элементов пробы, и бывает, когда в результате исследования элементы придут в негодное состояние. (Если, например, исследуется срок перегорания электрических ламп, приходится прокалить несколько электрических ламп). Так как снятие проб связано с расходами, статистику нужно стремиться принять решение на основе пробы с небольшим количеством элементов. Однако решение, принятое на основе пробы с небольшим количеством элементов, будет ошибочно с большей вероятностью, чем решение, принятое на основе пробы с большим количеством элементов. Ошибочное решение может привести к крупным потерям. Статистик должен выбрать такое число элементов пробы, при котором расходы (расходы снятия пробы плюс расходы из-за ошибочных решений) будут минимальными. Пусть Решение следует принимать на основе пробы с Пусть обозначаются суммарные расходы через Количество элементов пробы Такой вывод делается на основе рассуждений, проводимых по теории игр. Представим себе, что статистик и «природа» играют; в этой игре природа имеет право выбирать значение параметра Другой результат будет получен, если параметр
Вопросы для самопроверки по разделу 2 1. Что понимается под статистическим распределением выборки? 2. Какую функцию называют эмпирической функцией распределения? 3. Какими свойствами обладает эмпирическая функция? 4. Что такое гистограмма частот? 5. Какую оценку называют точечной? 6. Какую оценку называют несмещенной? 7. Какую оценку называют смещенной? 8. Какую оценку называют несмещенной оценкой математического ожидания? 9. Какую оценку называют смещенной оценкой генеральной дисперсии? 10. Какую оценку называют несмещенной оценкой генеральной дисперсии? 11. В чем суть метода моментов точной оценки неизвестных параметров заданного распределения? 12. В чем суть метода наибольшего правдоподобия? 13. Приведите примеры известных Вам интервальных оценок? 14. В чем суть метода произведений вычисления выборочной средней, дисперсии, асимметрии и эксцесса? 15. В чем суть метода сумм? 16. Что такое интервал конфиденции? 17. Что такое решающие функции?
|

 – некоторая случайная переменная с неизвестной
– некоторая случайная переменная с неизвестной  функцией распределения, с неизвестным параметром
функцией распределения, с неизвестным параметром  . Например,
. Например, 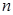 элементами
элементами  . Предположим, что возможные решения могут быть
. Предположим, что возможные решения могут быть 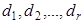 . Решение принимается на основе исследования пробы
. Решение принимается на основе исследования пробы  , возможными значениями которой являются возможные решения
, возможными значениями которой являются возможные решения  , если предположить, что значением параметра
, если предположить, что значением параметра  и в результате исследования пробы
и в результате исследования пробы  . Зная функции
. Зная функции  и
и  . Пусть такое математическое ожидание обозначается через
. Пусть такое математическое ожидание обозначается через  .
. было по возможности мало при любом значении
было по возможности мало при любом значении  , для которых значение
, для которых значение  является минимальным.
является минимальным. случайной переменной
случайной переменной  было минимальным.
было минимальным.


