Приложение теории суммирования случайного числа независимых случайных величин в задачах прогнозирования
Постановка задачи. В результате анализа объекта прогнозирования и прогнозного фона на периоде ретроспекции (периоде основания прогноза) установлено, что процесс развития системы может быть представлен ступенчатым процессом (последовательностью скачков, совершаемых в случайные моменты времени). Величина скачка
Рис. 2. Постановка задачи
Решение. Традиционным (основным) аналитическим аппаратом теории вероятностей и математической статистики является аппарат характеристических функций. Известно, что если  – действительная случайная величина, то существует комплексная случайная величина – действительная случайная величина, то существует комплексная случайная величина  (где (где 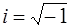 – мнимая единица, t – действительное число). – мнимая единица, t – действительное число).
Функция вида где E – символ математического ожидания, называется характеристической функцией случайной величины Характеристическая функция безразмерна, а параметр t имеет размерность, обратную размерности случайной величины Используем основные свойства характеристических функций для решения задачи, из условия решения которой известно, что выходной параметр системы y зависит как от случайного числа скачков n на периоде упреждения, так и от случайной величины Примем, что число скачков на периоде упреждения прогноза может быть определено законом Пуассона
с параметром Случайная же величина y (величина скачка) имеет стандартное нормальное распределение
Таким образом, чтобы получить закон распределения выходного параметра, необходимо рассмотреть распределение суммы пуассоновского числа стандартных нормальных величин. На основании мультипликативного свойства характеристической функции – характеристическая функция суммы независимых случайных величин равна произведению характеристических функций случайных величин, то есть, если
можно записать, что интегральная функция распределения
где Рассмотрим характеристическую функцию стандартного нормального распределения
Так как интеграл Отсюда характеристическая функция суммы пуассоновского числа стандартных нормальных величин имеет вид
Для определенности случай Тогда
Исходя из формулы обращения
тогда
В результате интегрирования получим искомую плотность распределения
В табл.6.1. приведем формулы для характеристических функций, наиболее часто встречающихся при решении практических задач. Решим поставленную задачу при условии, что величина скачка Характеристическая функция для функции распределения суммы случайного числа случайных величин
Таблица 1. Характеристические функции
В соответствии с формулой обращения запишем формулу для плотности распределения Изменяя порядок суммирования и интегрирования и учитывая, что симметричные законы распределения в характеристической функции не имеют членов, содержащих мнимую единицу, плотность распределения представим в виде
Используя табличный интеграл вида
при В табл. 2 приведены выражения для плотностей распределения выходной координаты при других условиях решениях поставленной задачи.
Таблица 2. Расчетные соотношения для плотности распределения величины Y
Необходимо помнить, что если
Дисперсия суммы может быть определена через второй момент
откуда
Рассмотрим еще один подход, при котором теоретическая вероятностная модель сочетается с экстраполяционной моделью на ЭВМ. Этот подход применяется тогда, когда вероятностную модель трудно составить из-за больших неопределенностей или модель трудно исследовать из-за ее сложности. При использовании этого метода неопределенности «реализуются» случайным образом путем использования процедуры Монте-Карло.
|

 (рис. 2) является случайной величиной, поведение которой описывается законом распределения
(рис. 2) является случайной величиной, поведение которой описывается законом распределения  . Число скачков n на периоде упреждения прогноза является случайным, распределенным по закону
. Число скачков n на периоде упреждения прогноза является случайным, распределенным по закону  . Требуется определить функцию распределения выходного параметра системы y.
. Требуется определить функцию распределения выходного параметра системы y.
 ,
, .
. независимы, одинаково распределены и не зависят от случайной величины n.
независимы, одинаково распределены и не зависят от случайной величины n. ,
, 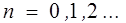
 , причем для распределения Пуассона справедливо соотношение
, причем для распределения Пуассона справедливо соотношение  .
. с параметрами
с параметрами  ,
,  и плотностью вероятности
и плотностью вероятности .
. , то
, то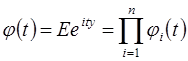 ,
, суммы случайного числа n случайных величин
суммы случайного числа n случайных величин 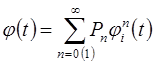 ,
, – характеристическая функция случайной величины
– характеристическая функция случайной величины 
 , то
, то  .
. .
. из рассмотрения исключим.
из рассмотрения исключим. .
. ;
; ,
, .
. .
.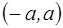 . Такое допущение о законе распределения скачка представляется целесообразным для коротких динамических рядов. Симметричность интервала не снижает общности рассуждений.
. Такое допущение о законе распределения скачка представляется целесообразным для коротких динамических рядов. Симметричность интервала не снижает общности рассуждений. .
.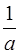 ,
, 

 ,
, 

 ,
, 

 ,
, 
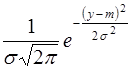 ,
, 
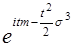
 .
. .
.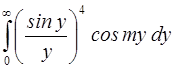 , находим плотность распределения выходной величины:
, находим плотность распределения выходной величины: ,
, , где
, где  и
и  , при
, при  ,
,  .
.

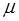








 и
и  , а
, а 
 , то для математического ожидания суммы случайного числа случайных слагаемых справедлива так называемая формула Вальда
, то для математического ожидания суммы случайного числа случайных слагаемых справедлива так называемая формула Вальда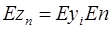 .
. ,
, .
.


