Принцип максимума неопределенности и стохастическое доминирование
В соответствии с теоретико-информационным подходом модели случайного эксперимента из рассматриваемых распределений предпочтение должно быть отдано тому закону распределения, который обладает большей неопределенностью. Используя эту концепцию и энтропию Шеннона в качестве меры неопределенности для сравнения и выбора соответствующих законов распределения, можно ввести частичную упорядоченность в множество одномерных функций распределения по энтропии. Назовем такое упорядочение
Так, например, пусть выборка из генеральной совокупности характеризуется математическим ожиданием Методами математической статистики не выявлено противоречия о принадлежности выборки нормальной генеральной совокупности с параметрами С этой целью определим значение дифференциальной энтропии для нормального закона с параметрами
и экспоненциальным параметром
Из сравнения результатов интегрирования следует, что нормальный закон распределения с параметрами
тогда и только тогда, когда коэффициент вариации В этом легко убедиться, рассмотрев неравенство
Весьма трудной проблемой является оценка показателей (характеристик) моделей процессов, статистическое обследование которых затруднено чрезвычайно малым объёмом испытаний. Сложность постановки в решении задач построения наилучших оценок для данной схемы и при данном объёме статистического материала обусловлена тем обстоятельством, что искомое решение часто в сильной степени зависит от конкретного типа распределения и объёма выборки. Можно указать на определенный круг задач теории малых выборок, для которых в первую очередь возникает задача выявления механизма формирования наблюдаемых значений Однако следует заметить, что в условиях малых выборок может наблюдаться, так называемый эффект малого объёма выборки, который состоит в том, что подбор подходящего модельного закона (нормального, равномерного и др.) для описания распределения исследуемой генеральной совокупности приводит к положительному результату для нескольких проверяемых гипотез (выдвигаемые гипотезы не опровергаются). Закон распределения в условиях малых выборок не всегда однозначно предопределен (в отличие от больших выборок), а процедура его подбора на основе теории проверки статистических гипотез в этих условиях приводит к тупиковой ситуации. В этих условиях представляется целесообразным использовать концепцию принципа максимума неопределенности (ввести Предположим, что в результате испытаний получены для равномерного на интервале
для экспоненциального распределения с параметром Используя значения параметров, определенные по выборке
где
Сопоставление выборочных значений энтропии
Таблица 2.
Заметим, что выборочные значения дифференциальных энтропий Используя законы распределений статистик можно получить зависимости для средних дифференциальных энтропий
Для равномерного на интервале и
тогда Используя табличный интеграл вида
после несложных преобразований находим Прежде чем перейти к выводу зависимости для
Выборочное среднее Следовательно,
где Нетрудно заметить, что в пределе при
Если в качестве параметров генеральной совокупности использовать их оценки, то представляется возможность упорядочить рассматриваемые распределения по усредненным значениям дифференциальных энтропии ( когда
или (после преобразований)
Заметим, что для пси-функции Эйлера где Условие стохастического доминирования (25) предполагает учёт объёма выборки Так, например, в табл. 3 представлены значения коэффициента Таблица 3. Значение константы
С увеличением объёма выборки значение константы Аналогичные условия можно записать и для других распределений.
Вопросы для самопроверки по разделу 4 1. На каком математическом понятийном аппарате могут быть построены формализованные модели неопределенности? 2. В чем состоит процесс экспериментирования? 3. Что является предметом изучения теории вероятностей? 4. Чем обусловлено введение меры неопределенности? 5. Что обычно используется в качестве меры неопределенности распределения вероятностей дискретной случайной величины? 6. Дайте определение энтропии Шеннона. 7. Что используется для сравнения различных распределений? 8. Что такое нечеткое множество? 9. Что понимается под субъективной вероятностью? 10. Какие существуют методы для оценок субъективной вероятности? 11. Какие основные требования должны удовлетворять понятие меры неопределенности? 12. В чем отличие простого линейного отношения порядка от усиленного? 13. Какой показатель используют в качестве характеризующего степень снижения уровня неопределенности? 14. Что характеризует показатель избыточности? 15. В чем заключается сущность аппроксимации субъективных вероятностей? 16. В чем суть принципа максимума неопределенности?
|

 – упорядочением и будем считать, что оно означает выполнение следующих условий:
– упорядочением и будем считать, что оно означает выполнение следующих условий: , (24)
, (24) для
для  и др.
и др.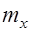 и дисперсией
и дисперсией  .
. и
и  и экспоненциальной совокупности с параметрами
и экспоненциальной совокупности с параметрами  . Анализ механизма формирования случайной величины
. Анализ механизма формирования случайной величины  не позволяет выдвинуть соображения теоретического характера, позволяющие выбрать для описания генеральной совокупности соответствующий закон распределения (нормальный или экспоненциальный). Требуется определить условия, при которых нормальный закон распределения доминирует над экспоненциальным и в соответствии с принципом максимума неопределенности является предпочтительным для описания генеральной совокупности.
не позволяет выдвинуть соображения теоретического характера, позволяющие выбрать для описания генеральной совокупности соответствующий закон распределения (нормальный или экспоненциальный). Требуется определить условия, при которых нормальный закон распределения доминирует над экспоненциальным и в соответствии с принципом максимума неопределенности является предпочтительным для описания генеральной совокупности.

 .
.
 ,
, .
. .
. . Это приводит к необходимости проверки гипотез о виде закона распределения исследуемой случайной величины. Процедура обоснованного сопоставления высказанной гипотезы с имеющимися выборочными данными
. Это приводит к необходимости проверки гипотез о виде закона распределения исследуемой случайной величины. Процедура обоснованного сопоставления высказанной гипотезы с имеющимися выборочными данными 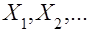 обычно осуществляется с помощью статистических критериев и статистик
обычно осуществляется с помощью статистических критериев и статистик  , Колмогорова,
, Колмогорова,  и других асимптотических критериев. В условиях малых выборок использовать предельные распределения этих статистик не представляется возможным.
и других асимптотических критериев. В условиях малых выборок использовать предельные распределения этих статистик не представляется возможным.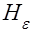 – упорядочение альтернативных законов распределений).
– упорядочение альтернативных законов распределений).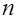 чисел
чисел  и проверка статистических гипотез о принадлежности функции распределения
и проверка статистических гипотез о принадлежности функции распределения 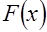 генеральной совокупности некоторому классу распределений (для определенности будем считать равномерному, нормальному и экспоненциальному) не выявила противоречий. Требуется определить условия, при которых каждый из рассматриваемых законов доминирует альтернативный. С этой целью определим значение дифференциальной энтропии и введем
генеральной совокупности некоторому классу распределений (для определенности будем считать равномерному, нормальному и экспоненциальному) не выявила противоречий. Требуется определить условия, при которых каждый из рассматриваемых законов доминирует альтернативный. С этой целью определим значение дифференциальной энтропии и введем 
 закона распределения;
закона распределения; для нормального распределения с параметрами
для нормального распределения с параметрами  ;
;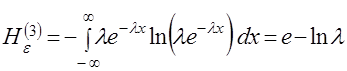
 .
. ,
,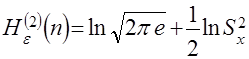 ,
,  ,
, ,
,  – оценка математического ожидания и выборочная дисперсия соответственно;
– оценка математического ожидания и выборочная дисперсия соответственно;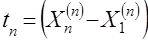 – размах выборки, определяемый по крайним членам вариационного ряда.
– размах выборки, определяемый по крайним членам вариационного ряда. ,
, 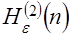 и
и 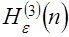 позволяет найти условия стохастического доминирования по энтропии рассматриваемых распределений, которые иллюстрируются табл. 2.
позволяет найти условия стохастического доминирования по энтропии рассматриваемых распределений, которые иллюстрируются табл. 2.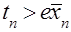
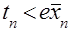
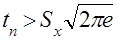



 зависят от различных статистик (размаха, выборочных средних и дисперсий) и, естественно, в разной степени чувствительны к объёму выборки
зависят от различных статистик (размаха, выборочных средних и дисперсий) и, естественно, в разной степени чувствительны к объёму выборки 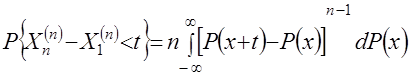 .
.
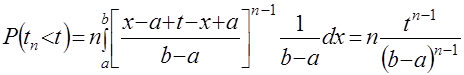 ,
, .
. ,
, .
. , заметим, что комплекс
, заметим, что комплекс  , для выборки из нормальной генеральной совокупности имеет
, для выборки из нормальной генеральной совокупности имеет  -распределение с
-распределение с  степенями свободы (распределение Пирсона). Используя это соотношение, преобразуем выражение для
степенями свободы (распределение Пирсона). Используя это соотношение, преобразуем выражение для 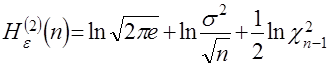 .
. ,
, – пси-функция Эйлера.
– пси-функция Эйлера. усреднённые «выборочные» значения энтропии
усреднённые «выборочные» значения энтропии  сходятся асимптотически к своим теоретическим значениям
сходятся асимптотически к своим теоретическим значениям ,
,  ,
, .
. -упорядочение для равномерного и экспоненциального распределения. Нетрудно заметить, что равномерное распределение доминирует над экспоненциальным в том случае,
-упорядочение для равномерного и экспоненциального распределения. Нетрудно заметить, что равномерное распределение доминирует над экспоненциальным в том случае, (25)
(25) .
. справедливо следующее функциональное соотношение
справедливо следующее функциональное соотношение  ,
, – постоянная Эйлера
– постоянная Эйлера  .
.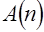 при
при 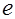 .
.


