Асимптотические свойства гипернормального распределения
При больших Для стандартных условий
Нетрудно проверить, что замена независимой переменной
Разделяя переменные и интегрируя, находим Отсюда следует где Осуществляя обратный переход от
Таким образом, функция квантилей гипернормального распределения асимптотически приближается к функции (13). Это свойство рассмотренных экстремальных распределений позволяет описать и прогнозировать с определенным уровнем доверия В общем случае можно показать, что дифференциальному уравнению (2) соответствует нелинейное дифференциальное уравнение, относительно квантильной функции
с граничными условиями
Для стандартных условий
решение которого, представленное в виде ряда, имеет следующий вид
Значения коэффициентов
Таблица 1. Значение коэффициентов
Математическое ожидание и дисперсия случайной величины
Значения функции предельного гипернормального распределения Математические ожидания и дисперсии для гипернормального распределения при малых Таблица 2. Математические ожидания и дисперсии
Остановимся еще на одном случае асимптотического поведения гипернормального распределения. Пусть
Разделяя переменные, находим где Интегрирование уравнения (10) позволяет убедиться в справедливости следующего утверждения. При больших значениях аргумента гипернормальное распределение асимптотически стремится к нормальному распределению с плотностью
|

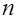 (более 10) дифференциальное уравнение (2) можно заменить приближенным и найти аналитическое решение для квантильной функции.
(более 10) дифференциальное уравнение (2) можно заменить приближенным и найти аналитическое решение для квантильной функции.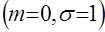 дифференциальное уравнение (2) при
дифференциальное уравнение (2) при  может быть представлено в виде
может быть представлено в виде 
 .
. позволяет преобразовывать это уравнение к виду
позволяет преобразовывать это уравнение к виду .
.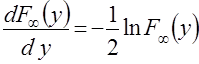 .
. ,
, и
и  – интегральный логарифм и интегральная показательная функция соответственно.
– интегральный логарифм и интегральная показательная функция соответственно. до
до  и от стандартных условий к естественным, можно получить функцию квантилей предельного гипернормального распределения
и от стандартных условий к естественным, можно получить функцию квантилей предельного гипернормального распределения ,
,  . (13)
. (13) экстремальные характеристики по ограниченной информации.
экстремальные характеристики по ограниченной информации.
 (14)
(14) ,
,  . (15)
. (15) , (16)
, (16)
 . (7)
. (7) , полученные в результате решения исходного уравнения, представлены в табл. 1.
, полученные в результате решения исходного уравнения, представлены в табл. 1.
 для предельного гипернормального распределения определяются по формулам
для предельного гипернормального распределения определяются по формулам ,
,
 .
. , аргументом которого является величина
, аргументом которого является величина  представлены в табличной форме.
представлены в табличной форме.
 представлены для стандартных условий
представлены для стандартных условий 
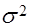
 (практически при
(практически при  ), естественным следствием из этого условия является
), естественным следствием из этого условия является  . Тогда дифференциальное уравнение (2) может быть представлено для стандартных условий
. Тогда дифференциальное уравнение (2) может быть представлено для стандартных условий  . (18)
. (18)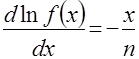 , (19)
, (19) – плотность гипернормального распределения.
– плотность гипернормального распределения. . (20)
. (20)


