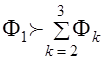Аппроксимация субъективных вероятностей
Сущность аппроксимации заключается в замене одних математических объектов другими в том или ином смысле близкими к исходным. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов. Развивая дедуктивно-аксиоматическое построение логики в целях обоснования математики, образно высказал эту мысль Бертран Рассел (1972–1970): «Хотя это может показаться парадоксальным – вся наука подчинена идее аппроксимации». Оценки субъективных вероятностей Одной из важнейших числовых характеристик субъективных вероятностей является максимальное математические ожидание его наибольшего значения. Функция распределения случайной величины, у которой при заданных первых двух моментах, максимально математическое ожидание наибольшего значения зависит от объёма выборки
Эта функция распределения зависит от объёма выборки и параметров исходного распределения
где Математическое ожидание наибольшего значения в этом случае определяется по формуле По определению математическое ожидание исходного распределения равно Действительно, Дисперсия в общем случае определяется следующим образом
Так, например, для оценок Фишборна (8)
После некоторых алгебраических преобразований можно получить следующую зависимость Тогда математическое ожидание наибольшего значения оценки определяется следующим образом Так, например, при Представляется целесообразным сравнить и интерпретировать этот результат с оценками Фишборна
Таблица 1. Сравнительный анализ субъектных вероятностей
В табл. 1 представлены результаты расчетов для различных отношений порядка предпочтения для случая учёта трех (
|

 по сути являются выборками из неизвестных законов распределения, поэтому было бы логично аппроксимировать законы распределения дискретных субъективных вероятностей непрерывными законами распределений случайных величин
по сути являются выборками из неизвестных законов распределения, поэтому было бы логично аппроксимировать законы распределения дискретных субъективных вероятностей непрерывными законами распределений случайных величин 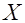 .
. определяется следующим образом
определяется следующим образом . (19)
. (19)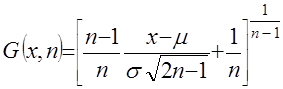 , (20)
, (20) – математическое ожидание и среднее квадратическое отклонение исходного распределения.
– математическое ожидание и среднее квадратическое отклонение исходного распределения. . (21)
. (21)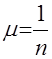 .
.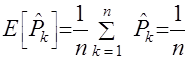 .
. .
.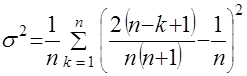 .
. . (22)
. (22) . (23)
. (23)
 .
. ,
,  ,
,  и другими оценками субъективных вероятностей (табл. 1).
и другими оценками субъективных вероятностей (табл. 1).