Теоретико-вероятностные основы построения распределений экстремальных значений
Распределение наибольшего Если известна функция распределения
Анализ экстремальных величин играет важную роль при изучении многих явлений и при решении прикладных задач. Заметим, что еще в 1709 г. Н. Бернулли рассматривал следующую имеющую отношение к статистике страхования задачу: В 1936 г. Мизес классифицировал исходные распределения, обладающие различными предельными распределениями наибольших величин, и получил достаточные условия, при которых справедливы предельные распределения. В настоящее время традиционно рассматривалось три таких предельных асимптотических распределения. Однако здесь необходимо отметить некоторые специфические ограничения асимптотических теорий экстремальных величин. Заметим, что в «классической» теории экстремальных значений при построении параметрических форм распределений экстремальных значений используется ключевая идея (постулат устойчивости), использованный ранее Фишером и Типпетом, заключающейся в следующем. Так как наибольшее наблюдение в выборке объёма то есть наибольшее наблюдение в выборке объёма Решение этого функционального уравнения относительно Тип I Тип II Тип III В действительности аналитические свойства исходного распределения редко известны и, следовательно, условия использования асимптотической теории экстремальных значений и постулата устойчивости не всегда соответствуют наблюдениям и практическим приложениям, при которых число наблюдаемых случайных величин невелико. Это приводит к необходимости использования принципа максимума неопределенности для выявления механизма формирования наблюдаемых экстремальных величин. Неопределенность исхода стохастического эксперимента обусловливает необходимость ее количественного описания и введения меры неопределенности. В качестве наиболее общей меры неопределенности распределения вероятностей случайной величины представляется целесообразным использовать энтропию Шеннона (меру относительной неопределенности ситуации, возможные исходы которой принадлежат множеству мощности континуум)
При выборе модели (закона распределения экстремальных величин) располагают, как правило, неполной (ограниченной) информацией о схеме (механизме) формирования наблюдаемых случайных величин. Незнание законов распределения случайных величин не исключает возможности их выбора из множества допустимых на основе использования меры неопределенности. Достаточным основанием для такого выбора являются следующие соображения. Приписывая случайной величине некоторые распределения, имеющие ряд свойств, совпадающих со свойствами действительного (неизвестного) распределения, мы совершаем по необходимости некоторый произвол: выбор одного из множества рассматриваемых распределений однозначно определяет и те характеристики, которые по условию неизвестны. Очевидно, что предпочтение надо отдать тому из рассматриваемых распределений, которое добавляет минимум информации к уже имеющейся. Другими словами, в процесс выбора модели должна оставаться максимальная неопределенность при учёте заданных ограничений. Эта концепция, известная под названием принципа неопределенности (максимума энтропии, принципа Джейнса и др.), предписывает выбирать из множества характеризующихся заданными свойствами распределений, удовлетворяющих данной системе ограничений, накладываемых на случайную величину, то, которое обладает наибольшей мерой неопределенности (наибольшей энтропией). Учитывая то обстоятельство, что многие задачи вероятностного анализа исходной статистической информации могут быть сформулированы в терминах порядковых статистик и связаны с изучением экстремальных значений, то представляется целесообразным распределение экстремальных случайных величин формировать на основе решения соответствующего класса вариационных задач. Процедуру построения модели экстремальных величин на основе принципа максимума неопределенности иллюстрирует следующий результат.
|

 или наименьшего
или наименьшего  значения в выборке из
значения в выборке из 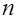 независимых одинаково распределенных случайных величин
независимых одинаково распределенных случайных величин  называется распределением экстремальных значений.
называется распределением экстремальных значений.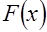 случайной величины
случайной величины 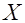 , то
, то ,
,  .
.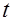 лет. Какова средняя продолжительность жизни последнего оставшегося в живых человека? Первым, кто начал исследование экстремальных величин в ХХ веке, был В. Борткевич. В 1925 г. Типпет вычислил вероятности наибольших значений в нормальной выборке для различных объёмов выборки вплоть до 1000. Исследование наибольших значений для других распределений было сделано Доддом. Далее Фреше было показано, что наибольшие величины, взятые из различных исходных распределений, обладают общими свойствами и могут иметь одинаковое предельное распределение.
лет. Какова средняя продолжительность жизни последнего оставшегося в живых человека? Первым, кто начал исследование экстремальных величин в ХХ веке, был В. Борткевич. В 1925 г. Типпет вычислил вероятности наибольших значений в нормальной выборке для различных объёмов выборки вплоть до 1000. Исследование наибольших значений для других распределений было сделано Доддом. Далее Фреше было показано, что наибольшие величины, взятые из различных исходных распределений, обладают общими свойствами и могут иметь одинаковое предельное распределение. можно рассматривать как наибольший член в выборке объёма
можно рассматривать как наибольший член в выборке объёма  , и так как из случая существования предельного распределения
, и так как из случая существования предельного распределения 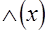 эти распределения будут стремиться к
эти распределения будут стремиться к  при
при 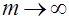 , то
, то  ,
, .
. .
.
 . (1)
. (1)


