Квантильная функция экстремального М-распределения (m-распределения)
Адекватность описания процессов, происходящих на экспериментальном уровне, предполагает полноту набора черт в отображении реального объекта. Однако учесть все реальные черты объекта невозможно, достаточно принять во внимание главные, позволяющие при четкой постановке задач статистического анализа, использовать математический аппарат построения экстремальных распределений экстремальных величин, базирующемся на эмпирическом факте и аксиоматическом подходе постулирования ожидаемого значения случайной величины В связи с этим рассмотрим экстремальное распределение экстремальной случайной величины, математическое ожидание исходной функции распределения которого характеризуется первым моментом. В этом случае, когда в результате статистического обследования ситуации выявлена лишь информация о среднем значении показателя, то экстремальное распределение максимального значения параметра определяется решением дифференциальным уравнением
при граничных условиях Справедливость этого положения вытекает из следующего утверждения. Пусть Тогда максимум энтропии достигается на распределении, удовлетворяющем дифференциальному уравнению (25) с функцией квантилей
Дифференциальное уравнение (26) является уравнением Эйлера-Лагранжа следующей вариационной задачи
Формальное интегрирование уравнения Эйлера-Лагранжа при
Используя подстановку
где Отсюда или где Из условия нормировки для функции распределения
Действительно, функции квантилей, определяемые из соотношения (29) имеют вид для исходной случайной величины и При Гипергеометрическая функция Гаусса в обобщенном виде может быть представлена в виде следующего ряда:
где При должен расходиться. По признаку Даламбера ряд (30) будет расходиться, если отношение
или после преобразований Для определения значения плотности в начальной точке
Левая часть уравнения в соответствии с определением
Ряд
которая после преобразования может быть представлена следующим образом:
Подстановка значения множителя Лагранжа в дифференциальное уравнение (28) позволяет убедиться в справедливости дифференциального уравнения (25) и функции квантилей (26). Кратко остановимся на методе определения математического ожидания наибольшего значения для рассматриваемого случая. Способом, аналогичным тому, который был применен при выводе формулы для определения значения плотности в нуле что
Для этого достаточно проинтегрировать функцию квантилей (26)
Представив гипергеометрическую функцию в виде ряда и переставив операции суммирования и интегрирования, найдем
Таблица 3. Значения суммы
В табл. 3 приведены значения суммы Функция квантилей экстремального распределения, определяемого дифференциальным уравнением (25) асимптотически
Действительно, в дифференциальном уравнении при Математическое ожидание случайной величины
Пример. Наблюдается дискретный случайный процесс Решение. В качестве оценки математического ожидания средней процесса при одном наблюдении естественно принять
|

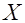 (ее математического ожидания
(ее математического ожидания  ).
). (25)
(25) .
. – функция распределения максимального значения из совокупности, определяемой случайной величиной
– функция распределения максимального значения из совокупности, определяемой случайной величиной  .
. . (26)
. (26) ,
,  ,
,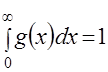 , (27)
, (27) ,
,  .
. дает экспоненциальный закон распределения, а при
дает экспоненциальный закон распределения, а при 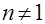 приводит к зависимости вида
приводит к зависимости вида . (28)
. (28) , интеграл (28) преобразуем к табличному
, интеграл (28) преобразуем к табличному ,
,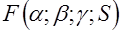 – гипергеометрическая функция Гаусса.
– гипергеометрическая функция Гаусса. (29)
(29)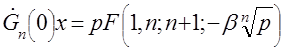 ,
,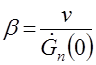 ,
,  .
.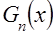 вытекает следующее соотношение
вытекает следующее соотношение .
.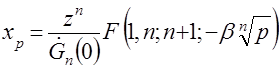
 для максимального значения из совокупности
для максимального значения из совокупности 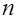 случайных величин.
случайных величин. ,
,  ,
,  .
. ,
, .
. ряд
ряд  (30)
(30)
 .
.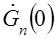 проинтегрируем соотношение (28) с учётом полученного значения для
проинтегрируем соотношение (28) с учётом полученного значения для .
. представляет собой произведения значения плотности распределения в нуле
представляет собой произведения значения плотности распределения в нуле 
 можно представить в виде разности двух рядов
можно представить в виде разности двух рядов ,
,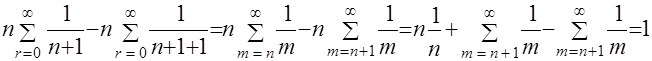 Таким образом
Таким образом 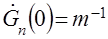 и множитель Лагранжа
и множитель Лагранжа
 .
.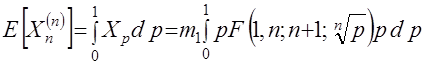 .
. .
.
 можно пользоваться, как будет показано ниже, асимптотическими свойствами полученных экстремальных распределений экстремальных величин).
можно пользоваться, как будет показано ниже, асимптотическими свойствами полученных экстремальных распределений экстремальных величин).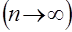 приближается к функции
приближается к функции . (31)
. (31)
 и дифференциальное уравнение имеет решение (29).
и дифференциальное уравнение имеет решение (29). в этом случае определяется следующим образом
в этом случае определяется следующим образом .
. , в первой точке наблюдения зафиксировано его значение
, в первой точке наблюдения зафиксировано его значение  . Каково математическое ожидание максимального значения во второй точке.
. Каково математическое ожидание максимального значения во второй точке. . Тогда используя табл. 3 средних значений
. Тогда используя табл. 3 средних значений  .
.


