Закон распределения коэффициента вариации
Идентификация случайных последовательностей, нестационарных случайных процессов и их производных по первым реализациям динамического ряда обусловливает необходимость введения в рассмотрение выборочного распределения коэффициента вариации. Коэффициентом вариации (коэффициентом изменчивости выборки) является отношение где Гауссово распределение не обладает тем свойством, что случайная величина может принимать только положительные значения, однако если В этом случае где Величина Не нарушая общности рассуждений и с целью использования зависимости (2) определим плотность распределения величины, обратной выборочному коэффициенту вариации Если каждая из независимых величин
Среднее арифметическое Поэтому можно показать, что плотность При При
После соответствующих преобразований плотность распределения величины Учитывая, что Теорема 5. Пусть имеет вид
|

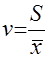 , (13)
, (13) и
и  – среднее значение и дисперсия выборки соответственно.
– среднее значение и дисперсия выборки соответственно. достаточно велико (более 3), то центральные моменты такого распределения будут с достаточной точностью равны соответствующим моментам полного нормального распределения.
достаточно велико (более 3), то центральные моменты такого распределения будут с достаточной точностью равны соответствующим моментам полного нормального распределения. ,
,  , (14)
, (14) – дисперсия величины
– дисперсия величины  .
. всюду непрерывна, а плотность вероятности
всюду непрерывна, а плотность вероятности  может быть определена следующим образом
может быть определена следующим образом  .
. , для выборки
, для выборки  из гауссовой генеральной совокупности с дисперсией
из гауссовой генеральной совокупности с дисперсией  и средним
и средним  .
. , то величины
, то величины  независимы и нормальны (0, 1). Таким образом, плотность вероятности величины
независимы и нормальны (0, 1). Таким образом, плотность вероятности величины  равна
равна . (15)
. (15) распределено нормально
распределено нормально  .
. можно определить следующим образом
можно определить следующим образом  . (16)
. (16)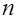 – нечетном
– нечетном  (17)
(17) . (18)
. (18) будет иметь вид
будет иметь вид  . (19)
. (19) , получаем следующий результат.
, получаем следующий результат. , тогда для выборки
, тогда для выборки  плотность распределения выборочного коэффициента вариации
плотность распределения выборочного коэффициента вариации  . (20)
. (20)


