Нормализация случайных величин
Не нарушая общности законов распределений задачи нормализация случайных величин будем решать применительно к стандартному нормальному распределению. Постановка задачи заключается в следующем. Если случайная величина в результате которого случайная величина Основной результат решения этой задачи можно сформулировать в виде следующего утверждения Теорема 7. Пусть
где Доказательство. Если уравнение однозначно разрешимо относительно
Квантиль (31) определяется следующим соотношением
где Следовательно, явное выражение для нормализующего преобразования приобретает вид (29). Значения коэффициентов В условиях малых выборок постановка задач нормализации случайных величин заключается в следующем. Случайные величины Эмпирическая функция распределения Таблица 2. Значения коэффициентов
По закону больших чисел при Это обстоятельство дает возможность непосредственно применить теорему 7 для нормализации случайных величин
Представление функции квантилей в виде ряда (системы уравнения относительно коэффициентов позволяет определить коэффициенты разложение нормализующего преобразования (29) после решения системы уравнений (35) для выборочных значений
|

 имеет закон распределения
имеет закон распределения  , то необходимо исходную случайную величину
, то необходимо исходную случайную величину 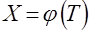 ,
,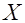 имела бы плотность гауссова распределения.
имела бы плотность гауссова распределения.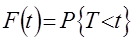 – функция распределения случайной величины
– функция распределения случайной величины 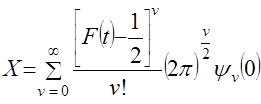 , (29)
, (29)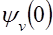 являются коэффициентами разложения в ряд квантили стандартного нормального распределения.
являются коэффициентами разложения в ряд квантили стандартного нормального распределения. (30)
(30)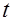 , то применив инверсный оператор
, то применив инверсный оператор 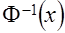 к обеим частям уравнения (30), получим
к обеим частям уравнения (30), получим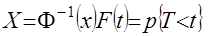 . (31)
. (31)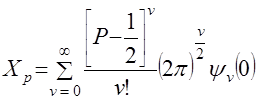 . (32)
. (32) ;
;  .
.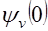 , вычисленные по рекуррентной формуле (29), представлены в табл. 2.
, вычисленные по рекуррентной формуле (29), представлены в табл. 2.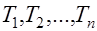 независимы и одинаково распределены с общей неизвестной функцией распределения
независимы и одинаково распределены с общей неизвестной функцией распределения 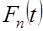 представляет собой ступенчатую функцию со скачками, кратными
представляет собой ступенчатую функцию со скачками, кратными 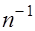 в точках, определяемых членами вариационного ряда
в точках, определяемых членами вариационного ряда 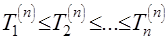 ,
,  (33)
(33)

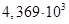
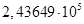
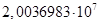


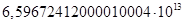
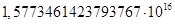
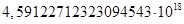
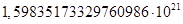
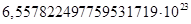
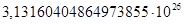
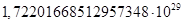
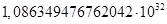



 для какого
для какого 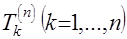
 . (34)
. (34)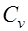 )
) 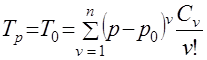 (35)
(35)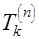 при
при 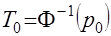 следующим образом
следующим образом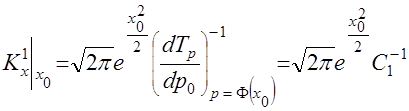 ,
,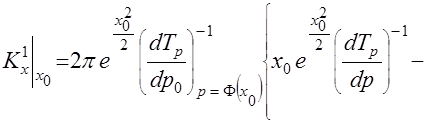
 и т.д.
и т.д.


