Функции потребительского спроса и информационно-статистические методы их структуризации
Описание поведения совокупного потребителя основано на ряде предположений о правилах выбора потребителем вектора продуктов Предварительно поясним содержание некоторых обозначений, принятых в теории предпочтений. Запись Постулируются следующие свойства отношения предпочтения совокупного потребителя. 1) Для любых неотрицательных векторов 2) Для любых 3) Для любого 4) Если 5) Если Отношение безразличия выделяет в пространстве всех векторов потребления множества (поверхности) безразличия. Поверхность безразличия Из аксиом 1–3 следует существование непрерывной скалярной функции Функцию полезности можно построить, зная отношение предпочтения, а точнее – поверхности безразличия Аксиома 4 об отношении предпочтения приводит к положительности частных производных функции полезности
Если при этом функция Следующий шаг в построении теории потребления – предположение о том, что совокупный потребитель рационально расходует свои денежные средства. В терминах предпочтений это предложение звучит так: потребитель, исходя из уровня цен
Геометрически это означает, что потребитель выбирает вектор В результате решения задачи (1) получается вектор-функция
(после вертикальной черты в фигурных скобках записываются условия, при которых отыскивается экстремум). Функция (1) называется функцией спроса. Она обладает рядом важных свойств: 1) Монотонно возрастающее преобразование функции полезности не изменяет функцию спроса. 2) Однородность нулевой степени:
то есть спрос не меняется при пропорциональном изменении всех цен и дохода (в отличие от однородности первой степени производственной функции). 3) Условие Слуцкого: если образовать выражения
то оказывается, что Выражение (4) именуют остаточной изменчивостью потребления 4) Отрицательная определенность квадратичной формы с матрицей
( Все эти свойства выводятся формальными методами как следствия свойств функции полезности. Укажем еще одно свойство функций спроса, установленное непосредственно по экономической статистике. 5) Не все эластичности спроса по доходу должны быть единичными: существует такой продукт
В противном случае структура вектора спроса не менялась бы с изменением дохода а это противоречит экономическим наблюдениям. В проекции на функцию полезности условие (8) означает невозможность _пиисания потребительских предпочтений с помощью однородной функции полезности и это отличает ее от производственной функции. Приведем теперь пример конкретной функции спроса. Для этого зададим функцию полезности в виде:
где
Функции (8) получаются одна из другой монотонно возрастающим преобразованием, поэтому и порождающее их отношение предпочтения и порождаемая ими функция спроса единственны.
Решение задача (1) с функциями (8) дает
Для этих функций выполняются все пять указанных выше свойств. Функции (9) построены, исходя из второго варианта функции полезности (8). За основу были взяты следующие предположения, оправдываемые статистикой: 1) по каждому продукту существует минимальный уровень потребления 2) минимальный уровень потребления всегда обеспечивается 3) оставшиеся после обеспечения минимального потребления денежные средства распределяются по видам продуктов в фиксированной пропорции. Параметры Как в экономической, так и социальной теориях различают два подхода к оценке соизмерения различных товаров и услуг: кардиналистский (количественный) и ординалистский (порядковый, качественный). Количественный подход основан на представлении о возможности измерения полезности различных благ непосредственно в каких-либо единицах полезности (ютилах). Предельная полезность характеризует прирост общей полезности (сумму полезностей) при увеличении объёма потребления данного блага на одну единицу. В основе процессов и явлений, формирующих закономерности рыночного спроса в микроэкономике лежит здравый смысл поведения покупателя. В любой данный период каждый покупатель продукта получает меньше удовлетворения (выгоды, полезности) от каждой последующей единицы продукта. Отсюда следует, что потребление подвержено действию принципа убывающей предельной полезности, следствием из которого является то, что потребители будут покупать дополнительные единицы продукта лишь при условии снижения его цены. При анализе полезности товаров и предпочтений покупателя в экономике исходят из следующего предположения: любое благо распределяется между различными альтернативными целями его использования в таких пропорциях, чтобы предельная полезность при пользовании его во всех целях была одинаковой. В формализованном виде этом можно записать следующим образом
где При проведении экономического анализа для формирования функции спроса весьма важно знать динамику изменения предельной полезности Общий вид таких моделей может быть представлен зависимостью
где
В частном случае зависимость (11) может принимать вид
Основными наиболее распространенными методами оценивания параметров моделей (8) могут быть: ü метод максимального правдоподобия (в частном случае метод наименьших квадратов); ü метод максимальной апостериорной вероятности (байесовский метод); ü минимаксный метод. Условия и процедуры применения этих методов подробно изложены в литературе по математической статистике. Следует заметить, что на использование каждого метода накладываются определённые ограничения. Так, например, использование метода наименьших квадратов ограничивается его чувствительностью к отклонению результатов наблюдений от нормального закона; применение метода максимального правдоподобия характеризуется сложными вычислительными процедурами; байесовский подход требует использования априорной информацией; кроме того, байесовские оценки не совпадают с оценками максимального правдоподобия при использовании малых выборок: мерой оптимальности оценок в минимаксного методе служат функции потерь, выбор которых неоднозначен. Кроме того, все эти методы с точки зрения прогностики не чувствительны к эффекту дисконтирования. Трудности, связанные с необходимостью учёта дисконтирования и использования нескольких решающих правил, генерируемых применением различных методов, обусловливают потребность поиска другого подхода к решению задачи оценивания параметров моделей. Для решения задачи оценивания параметров модели с учётом изложенного представляется целесообразным использование информационных критериев. Не нарушая общности рассуждения, можно показателю полезности
Зависимость (13) может рассматриваться как мера неопределённости знания о состоянии объекта при условии, что это состояние оценивается распределением Использование функции неточности основывается на том, что разность
можно рассматривать как меру погрешности при замене истинного значения Пусть оценка параметров производится по результатам В качестве модели процесса сначала рассмотрим относительно простое уравнение (9). В этой зависимости только два неизвестных параметра – следовательно, Подставляя (14) в (13), получим функционал неточности в виде
Для отыскания неизвестного параметра
Отсюда следует, что Для определения значения Возможно использование совместно с рассматриваемым методом и метод наименьших квадратов. Такой подход, как нетрудно заметить даст следующий результат:
Таким образом, применение рассматриваемого экстремального принципа для определения параметров модели даёт решение задачи с точностью до одного свободного члена. В силу свойств рассматриваемого информационного критерия выбор этих параметров не оказывает влияния на значение оптимизируемого параметра. Для определения свободного параметра представляется целесообразным использовать дополнительные условия (граничные условия, условие минимума квадрата отклонений и др.). Вопросы для самопроверки по разделу 7 1. Дайте определение понятию «критерий». 2. При помощи какой функции можно сравнивать различные доли системы? 3. Что такое функции некомфортности? 4. Что понимается под объединением (свертыванием) векторного критерия оптимальности? 5. Что такое весовые коэффициенты? 6. Что такое субъективная вероятность? 7. Что такое качественная вероятность? 8. В чем сущность метода парных сравнений? 9. Как определяется коэффициенты линейной средней квадратической регрессии для генеральной совокупности? 10. Что является целью регрессионного анализа? 11. Приведите пример применения информационно-статистических методов к задачам анализа функции спроса?
Заключение Развитие сложных систем неразрывно связано с внедрением новейших научных достижений и реализацией прогрессивных информационных технологий. Перспектива кардинального решения этих проблем непосредственно связана с разработкой и внедрением теоретических основ системно-информационного анализа сложных систем и процессов. Анализ совокупности научных проблем, возникающих в процессе научных исследований и разработок, позволяет заметить, что большинство из них связано с постановкой и решением нетривиальных задач. Процедура постановки и решения этих задач затрагивает целый ряд областей фундаментального и прикладного значения, в каждой из которых в настоящее время ведутся интенсивные исследования.
3.2. Опорный конспект. 26 Раздел 1. Система двух случайных величин. 26 Введение. 26 § 1. Законы распределения случайных величин. 27 § 1.1. Закон равномерного распределения вероятностей. 27 § 1.2. Нормальное распределение. 29 § 1.3. Распределение «хи-квадрат». 31 § 1.4. Распределение Стьюдента. 35 § 1.5. Распределение F Фишера-Снедекора. 36 § 1.6. Показательное распределение. 39 § 1.7. Гамма-распределение и распределение Эрланга. 40 § 1.8. Функция надежности. 47 § 2. Система двух случайных величин. 48 § 2.1. Закон распределения вероятностей дискретной двумерной случайной величины.. 49 § 2.2. Функция распределения двумерной случайной величины.. 50 § 2.3. Вероятность попадания случайной точки в полуполосу. 52 § 2.4. Вероятность попадания случайной точки в прямоугольник. 52 § 2.5. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности). 53 § 2.6. Нахождение функции распределения системы по известной плотности распределения 55 § 2.7. Условные законы распределения составляющих системы случайных величин. 57 § 2.8. Условное математическое ожидание. 60 § 2.9. Зависимые и независимые случайные величины.. 61 § 2.10. Числовые характеристики системы двух случайных величин. 61 § 2.11. Коррелированность и зависимость случайных величин. 62 § 2.12. Линейная регрессия. 62 Раздел 2. Элементы математической статистики. 65 § 1. Статистическое распределение выборки. 65 § 2. Эмпирическая функция распределения. 65 § 3. Полигон и гистограмма. 67 § 3.1. Дискретное распределение признака § 3.2. Непрерывное распределение признака § 4. Точечные оценки. 68 § 5. Метод моментов. 70 § 6. Метод наибольшего правдоподобия. 71 § 6.1. Дискретные случайные величины.. 71 § 6.2. Непрерывные случайные величины.. 72 § 7. Интервальные оценки. 74 § 8. Метод произведений вычисления выборочной средней и дисперсии. 75 § 8.1. Равноотстоящие варианты.. 75 § 8.2. Неравноотстоящие варианты.. 77 § 9. Метод сумм для вычисления выборочной средней и дисперсии. 78 § 10. Асимметрия и эксцесс эмпирического распределения. 79 § 10.1. Метод произведений. 79 § 10.2. Метод сумм.. 80 11. Исследование гипотез. 82 § 12. Некоторые общие понятия теории оценки. 85 § 12.1. Оценка математического ожидания. 85 § 12.2. Оценка дисперсии. 85 § 12.3. Оценка функций распределения и плотности. 86 § 13. Интервал конфиденции. 87 § 14. Решающие функции. 87 Раздел 3. Вероятностные методы прогнозирования. 89 § 1. Приложение теории суммирования случайного числа независимых случайных величин в задачах прогнозирования. 90 § 2. Ориентированный процесс случайного блуждания как метод вероятностного моделирования 95 Раздел 4. Структуризация вероятностных моделей неопределенности. 100 § 1. Меры неопределенности и субъектные вероятности. 100 § 2. Аппроксимация субъективных вероятностей. 109 § 3. Принцип максимума неопределенности и стохастическое доминирование. 111 Раздел 5. Экстремальные распределения экстремальных случайных величин. 117 Введение. 117 § 1. Теоретико-вероятностные основы построения распределений экстремальных значений. 117 § 2. Гипернормальное распределение (HN-распределение). 119 § 3. Асимптотические свойства гипернормального распределения. 122 § 4. Квантильная функция экстремального М-распределения (m -распределения). 124 § 5. Экстремальные распределения минимальных величин. 129 Раздел 6. Статистики малых выборок. 131 Введение. 131 § 1. Метод построения законов распределения статистик. 131 § 2. Статистики малых выборок из гауссовых генеральных совокупностей. 133 § 3. Закон распределения коэффициента вариации. 135 § 4. Непараметрические статистики малых выборок. 137 § 5. Нормализация случайных величин. 140 § 6. Энтропийные метрики. 143 Раздел 7. Примеры применения вероятностных методов прогнозирования сложных систем.. 145 Введение. 145 1. Формализация слабоструктурированных и неструктурированных задач экономики 146 2. Производственные функции и информационно-статистические методы их структуризации 162 3. Функции потребительского спроса и информационно-статистические методы их структуризации. 170 Заключение. 177
* Максвелл Джеймс Клерк (1831–1879) – шотландский физик, член Лондонского Королевского общества. * От лат. Continuum – непрерывный («математика континуума») употребляется тогда, когда говорят о теориях, связанных с понятием непрерывности, противопоставляя их «математике дискретной». * MLM – Marcos Lopis Martyschenko
|

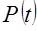 . Эти правила можно сформулировать с помощью так называемого слабого отношения предпочтения
. Эти правила можно сформулировать с помощью так называемого слабого отношения предпочтения  («предпочтительнее, чем …, или равноценен», «не менее предпочтителен, чем …»).
(«предпочтительнее, чем …, или равноценен», «не менее предпочтителен, чем …»).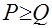 означает, что потребитель либо предпочитает вектор
означает, что потребитель либо предпочитает вектор 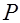 вектору
вектору  , либо не делает между ними различия. Векторы
, либо не делает между ними различия. Векторы 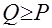 . Потребитель предпочитает вектор
. Потребитель предпочитает вектор 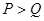 ), если
), если  из условий
из условий 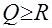 следует
следует  (транзитивность слабого отношения предпочтения).
(транзитивность слабого отношения предпочтения).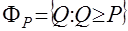 и «непредпочтительное» множество
и «непредпочтительное» множество 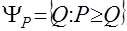 замкнуты (предельные переходы не выводят из соответствующего множества).
замкнуты (предельные переходы не выводят из соответствующего множества).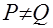 , то
, то 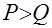 (увеличение хотя бы одной компоненты вектора
(увеличение хотя бы одной компоненты вектора 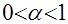 выполняется отношение
выполняется отношение  движение по отрезку, соединяющему некоторый вектор
движение по отрезку, соединяющему некоторый вектор 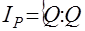 ~
~ 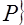 заданному вектору
заданному вектору  и
и 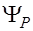 .
.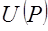 , для которой неравенство
, для которой неравенство  эквивалентно отношению
эквивалентно отношению  в том смысле, что более предпочтительным вектором соответствуют большие значения функции, а равноценным векторам – равные значения, и обратно. Такая функция получила название функции полезности. Она более экономно описывает выбор потребителя, чем исходное отношение предпочтения.
в том смысле, что более предпочтительным вектором соответствуют большие значения функции, а равноценным векторам – равные значения, и обратно. Такая функция получила название функции полезности. Она более экономно описывает выбор потребителя, чем исходное отношение предпочтения.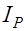 . Эти поверхности объявляются поверхностями уровня функции полезности:
. Эти поверхности объявляются поверхностями уровня функции полезности: 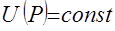 для всех
для всех  . Значение константы задается так, чтобы более предпочтительному вектору
. Значение константы задается так, чтобы более предпочтительному вектору 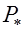 , маркирующему поверхность безразличия, соответствовало большее значение константы. Таких соответствий можно задать сколько угодно, поэтому одно отношение предпочтения порождает бесконечное множество функций полезности. Все эти функции по построению имеют одинаковые поверхности уровня (но с разными значениями функции на одной и той же поверхности), они могут быть получены из одной функции полезности
, маркирующему поверхность безразличия, соответствовало большее значение константы. Таких соответствий можно задать сколько угодно, поэтому одно отношение предпочтения порождает бесконечное множество функций полезности. Все эти функции по построению имеют одинаковые поверхности уровня (но с разными значениями функции на одной и той же поверхности), они могут быть получены из одной функции полезности 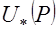 суперпозицией со строго возрастающей функцией
суперпозицией со строго возрастающей функцией  скалярного аргумента:
скалярного аргумента: 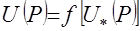 . В некоторых построениях функция полезности принимается как исходная, и тогда ее значения трактуются как мера «удовольствия» от потребления различных наборов продуктов.
. В некоторых построениях функция полезности принимается как исходная, и тогда ее значения трактуются как мера «удовольствия» от потребления различных наборов продуктов.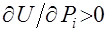 (если она таковыми обладает). Аксиома 5 влечет строгую квазивогнутость
(если она таковыми обладает). Аксиома 5 влечет строгую квазивогнутость 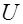 :
: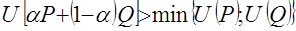
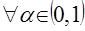 .
.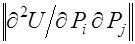 – отрицательно определенная. Отмеченные свойства функции полезности роднят ее с производственной функцией.
– отрицательно определенная. Отмеченные свойства функции полезности роднят ее с производственной функцией. и своего дохода
и своего дохода 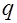 , делает такой выбор вектора продуктов с компонентами
, делает такой выбор вектора продуктов с компонентами  , который является для него наиболее предпочтительным из всех наборов со стоимостью, равной
, который является для него наиболее предпочтительным из всех наборов со стоимостью, равной 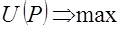 по
по  . (1)
. (1) , соответствующий точке касания плоскости равной стоимости с некоторой поверхностью безразличия.
, соответствующий точке касания плоскости равной стоимости с некоторой поверхностью безразличия.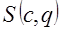 , связывающая вектор конечного потребления
, связывающая вектор конечного потребления  и доходом
и доходом 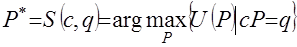 (2)
(2) , (3)
, (3)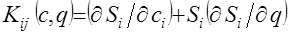 ,
, 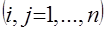 , (4)
, (4) ,
, 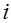 -го продукта при компенсированном изменении цены
-го продукта при компенсированном изменении цены 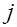 -го продукта. Компенсированным называют такое изменение цены
-го продукта. Компенсированным называют такое изменение цены  , которое сопровождается изменением дохода
, которое сопровождается изменением дохода  по новой цене.
по новой цене.
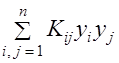 при
при  (6)
(6)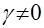 – скаляр,
– скаляр, 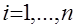 ).
).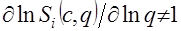 . (7)
. (7) ,
, 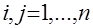 ,
,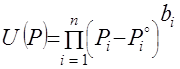 или
или  , (8)
, (8) ,
, 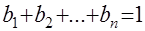 ,
,  ,
, 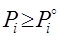 ,
,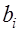 – параметры, соизмеряющие полезность различных продуктов;
– параметры, соизмеряющие полезность различных продуктов; – минимальный уровень потребления.
– минимальный уровень потребления.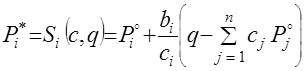 ,
, 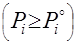 ,
,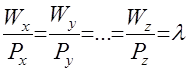 , (10)
, (10)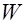 – предельная полезность;
– предельная полезность;  ,
,  ,
,  – цена товаров
– цена товаров  ,
,  ,
, 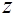 ;
; 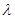 – коэффициент пропорциональности предельной полезности его цене.
– коэффициент пропорциональности предельной полезности его цене.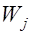 при увеличении объёма потребления на
при увеличении объёма потребления на 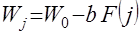 , (11)
, (11)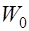 – начальное значение полезности;
– начальное значение полезности;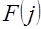 – функция числа объёма потребления, характеризующая изменение предельной полезности при увеличении объёма потребления на
– функция числа объёма потребления, характеризующая изменение предельной полезности при увеличении объёма потребления на 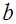 – параметр процесса.
– параметр процесса.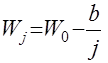 . (12)
. (12)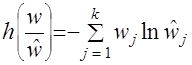 . (13)
. (13)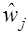 , в то время как истинное состояние характеризуется состоянием
, в то время как истинное состояние характеризуется состоянием 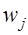 . В частном случае
. В частном случае  выражение (13) вырождается в энтропию Шеннона. Таким образом, использование функции неточности (13) для решения задач оценивания параметров модели можно рассматривать как распространение экстремального принципа формирования закона распределения на соответствующий класс задач.
выражение (13) вырождается в энтропию Шеннона. Таким образом, использование функции неточности (13) для решения задач оценивания параметров модели можно рассматривать как распространение экстремального принципа формирования закона распределения на соответствующий класс задач.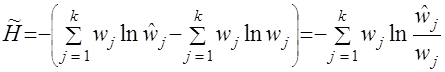 (14)
(14)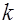 серий
серий 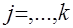 наблюдений за изменениями полезности, каждой из которых соответствует неизвестное значение показателя полезности.
наблюдений за изменениями полезности, каждой из которых соответствует неизвестное значение показателя полезности. ,
,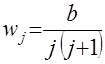 . (15)
. (15)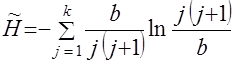 . (16)
. (16)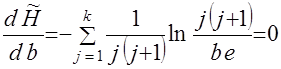 . (17)
. (17) . (18)
. (18) , соответственно
, соответственно 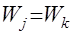 (в этом случае аппроксимирующая зависимость проходит через конечную точку и эффект дисконтирования исключается);
(в этом случае аппроксимирующая зависимость проходит через конечную точку и эффект дисконтирования исключается); 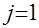 , в этом случае зависимость проходит через начальную точку; и точку, в которой достигается
, в этом случае зависимость проходит через начальную точку; и точку, в которой достигается 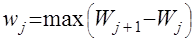 .
.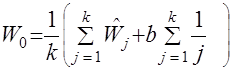 . (19)
. (19)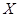 .... 67
.... 67


