Экстремальные распределения минимальных величин
Рассмотрим некоторые особенности построения экстремальных распределений минимальных величин. Экстремальной распределение минимальной величины
определяется решением дифференциального уравнения
где Это дифференциальное уравнение является уравнением Эйлера-Лагранжа вариационной задачи, аналогичной задаче (4, …, 9) Отличие в постановке вариационной задачи заключается в замене связи (9) зависимостью
Нелинейное дифференциальное уравнение (33) удовлетворяет естественным краевым условиям и полностью определяется первыми двумя центральными моментами Свойства функции При значениях аргумента
При В качестве примера определим математическое ожидание размаха Если выборка из генеральной совокупности характеризуется только математическим ожиданием, то экстремальное распределение
определяется в результате решения дифференциального уравнения
где Дифференциальное уравнение (36) удовлетворяет краевым условиям:
и полностью определяется параметрами Экстремальному распределению этого типа соответствует функция квантилей, отображающая Математическое ожидание случайной величины При
Особенности экстремальных распределений вытекают из следующих соображений. Дифференциальное уравнение является уравнением Эйлера-Лагранжа вариационной задачи, аналогичной задаче (27). Отличие в постановке задачи заключается в замене последней голономной связи Интегрирование дифференциального уравнения (36) позволяет получить функцию квантилей (38), а осуществление предельного перехода
Вопросы для самопроверки по разделу 5 1. Что называется распределением экстремальных значений? 2. Как используется принцип максимума неопределенности при формировании наблюдаемых экстремальных величин? 3. Приведите примеры построения модели экстремальных величин на основе принципа максимума неопределенности? 4. Какие есть особенности построения экстремальных распределений минимальных величин?
|


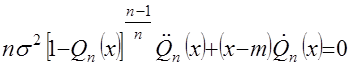 (32)
(32) – математическое ожидание и дисперсия совокупности исходных случайных величин.
– математическое ожидание и дисперсия совокупности исходных случайных величин. (33)
(33) (34)
(34) исходной случайной совокупности и параметром
исходной случайной совокупности и параметром 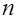 (объёмом выборки).
(объёмом выборки). аналогичны свойствам функции
аналогичны свойствам функции 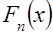 , поэтому экстремальному распределению этого типа соответствует функция распределения
, поэтому экстремальному распределению этого типа соответствует функция распределения  экстремальное распределение
экстремальное распределение  асимптотически сближается с нормальным распределением с плотностью:
асимптотически сближается с нормальным распределением с плотностью: .
. экстремальное распределение
экстремальное распределение  . (35)
. (35) для
для 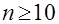
 .
.
 , (36)
, (36) – математическое ожидание совокупности исходных случайных величин.
– математическое ожидание совокупности исходных случайных величин. (37)
(37) в
в 
 . (6.38)
. (6.38) определяется по зависимости:
определяется по зависимости: 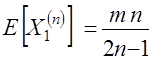 . (39)
. (39) асимптотически сближается с равномерным
асимптотически сближается с равномерным  с математическим ожиданием
с математическим ожиданием . (40)
. (40) зависимостью
зависимостью  , определяющей функцию распределения наименьшего значения
, определяющей функцию распределения наименьшего значения  .
. зависимость (41). Характерной особенностью этих распределений является то, что они реализуются в классе финитных функций (усеченных слева). Следует также заметить, что зависимости для математических ожиданий наименьших значений (39) и (41) могут найти практическое применение при экспресс-оценке выборок из неизвестной генеральной совокупности.
зависимость (41). Характерной особенностью этих распределений является то, что они реализуются в классе финитных функций (усеченных слева). Следует также заметить, что зависимости для математических ожиданий наименьших значений (39) и (41) могут найти практическое применение при экспресс-оценке выборок из неизвестной генеральной совокупности.


