Метод построения законов распределения статистик
Идентификация случайных процессов, экспресс-оценка момента их «разладки» и прогнозирование дальнейшего их развития на основе первых наблюдений может быть сведена к процедуре проверки статистических гипотез. В соответствии с этим в тестах проверки небольших последовательностей случайных чисел (коротких динамических рядов) необходимо использование некоторых функций от наблюдаемых случайных величин по терминологии Р.Фишера (статистик), законов их распределений и критериев проверки гипотез. Многие вводимые далее в рассмотрение статистики имеют форму
дифференцируя, находим, что отношение
Такой прием называется рандомизацией [12] и означает рассмотрение знаменателя величины Используя метод рандомизации, докажем ряд теорем, которые окажутся полезными в дальнейших приложениях. Теорема 1. Пусть и
Доказательство. В соответствие с (2)
В последнем выражении интеграл является интегралом от плотности гамма-распределения и, естественно, равен единице. После несложных преобразований соотношение (6) может быть преобразовано в выражение для плотности (5). Теорема доказана. Из теоремы 1. в силу большой общности гамма-распределения вытекает ряд полезных следствий, позволяющих оценить момент разладки простейшего потока, потока Эрланга и др. Так, например, если отношение Если случайная величина
где
|

 , где
, где 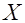 и
и  независимые случайные величины и
независимые случайные величины и  . Обозначим их функции распределения через
. Обозначим их функции распределения через 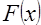 и
и 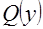 , а их плотности через
, а их плотности через  и
и 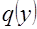 соответственно. Так как величина
соответственно. Так как величина 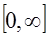 , и поэтому
, и поэтому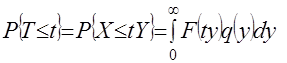 , (1)
, (1)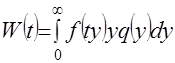 . (2)
. (2)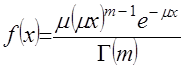 (3)
(3) , (4) тогда отношение
, (4) тогда отношение  . (5)
. (5)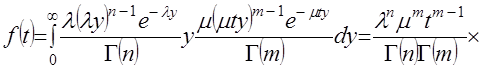
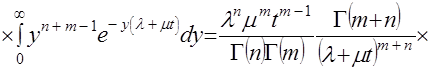
 . (6)
. (6)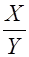 представляет собой отношение двух показательно распределенных случайных независимых величин с параметром
представляет собой отношение двух показательно распределенных случайных независимых величин с параметром 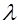 , то плотность их отношения
, то плотность их отношения  имеет вид
имеет вид 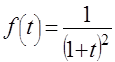 . (7)
. (7)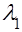 , а величина
, а величина 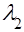 , то плотность их отношения имеет вид
, то плотность их отношения имеет вид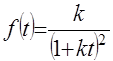 , (8)
, (8) .
.


