Непараметрические статистики малых выборок
Универсальный характер нормального (гауссова) распределения и полнота теоретических исследований, относящихся к нему, обусловливают необходимость обратиться к задаче анализа стохастического процесса, описывающего динамику изменения параметров процесса для тех случаев, когда соответствующие оценки и допущения предполагают получение анализируемых данных в виде случайных величин, распределенных по закону Гаусса. С этой целью представляется целесообразным предварительно проверить гипотезу о принадлежности исходных данных нормальной совокупности и, если такая гипотеза будет отвергнута, то найти соответствующее нормализующее преобразование выборочных данных, позволяющее решать задачу прогноза, оценку эффективности принимаемых решений и др. Заметим, что эта задача в силу ограниченного объёма исходной информации должна решаться в условиях малых выборок. В тестах проверки небольших последовательностей случайных чисел на нормальность представляется целесообразным использовать непараметрические статистики. Порядок их формирования заключается в следующем. По выборке объёма
где
Нетрудно заметить, что алеф статистики Для дальнейшего использования непараметрических статистик необходимо знать законы их распределения. С этой целью используем следующую теорему, приводимую без доказательств, доказательство которой произведено А.А.Клавдиевым. Теорема 6. Пусть случайные величины Аналогичная теорема имеет место и для случая Теорема 7. Пусть случайные величины
имеет вид Сформированные непараметрические статистики могут быть использованы для проверки гипотезы о принадлежности выборки нормальной генеральной совокупности. Для выборки объёма
для выборок объёма
Границы критической области При этом принятие решения о виде закона распределения осуществляется на основе сравнения расчетного значения критерия Если то нет оснований отвергнуть выдвинутую гипотезу. Рассмотренный метод проверки гипотезы о виде закона распределения, основанный на использовании непараметрических статистик, дополним еще одним, использующим так называемый Порядок использования
если Коэффициенты Статистика критерия имеет вид где Для получения выводов о справедливости гипотезы о принадлежности выборки генеральной нормальной совокупности необходимо задаться доверительной вероятностью Таким образом, введенные в рассмотрение тестовые статистики позволяют идентифицировать короткие динамические ряды и малые выборки из гауссовых совокупностей по ограниченной информации. Область применения этих статистик не ограничивается только нормальными совокупностями. Если функция распределения не является функцией гауссова распределения, то можно произвести нормализацию случайных величин и использовать приведенные выше статистики и законы их распределения для идентификации законов распределения малых выборок.
|

 формируется вариационный ряд
формируется вариационный ряд  . Для нормального закона распределения, используя известные соотношения
. Для нормального закона распределения, используя известные соотношения ,
, 
 – стандартная нормально распределенная случайная величина с параметрами
– стандартная нормально распределенная случайная величина с параметрами  и
и  , можно получить непараметрическое преобразование в виде
, можно получить непараметрическое преобразование в виде ,
, 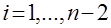 . (21)
. (21)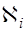 не зависят от параметров исходного (гипотетического) распределения, а зависят только от стандартных нормально распределенных величин и объёма выборки.
не зависят от параметров исходного (гипотетического) распределения, а зависят только от стандартных нормально распределенных величин и объёма выборки. и
и 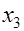 взаимно независимы и распределены одинаково нормально, тогда плотность распределения отношения
взаимно независимы и распределены одинаково нормально, тогда плотность распределения отношения  имеет вид
имеет вид  . (22)
. (22) .
. взаимно независимы и распределены одинаково нормально и пусть
взаимно независимы и распределены одинаково нормально и пусть  – вариационный ряд, где
– вариационный ряд, где  и
и  , тогда плотность распределения статистики
, тогда плотность распределения статистики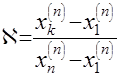 (23)
(23) . (24)
. (24) интегральная функция распределения
интегральная функция распределения  -статистики имеет вид
-статистики имеет вид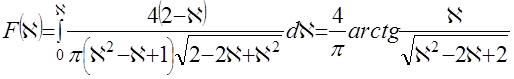 , (25)
, (25)
 . (26)
. (26) .
. с критерием
с критерием  .
.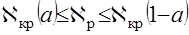 , (27)
, (27)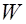 -критерий нормальности Шапиро-Уилка.
-критерий нормальности Шапиро-Уилка.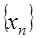 формируется вариационный ряд
формируется вариационный ряд  . Далее вычисляется сумма взвешенных с коэффициентами
. Далее вычисляется сумма взвешенных с коэффициентами 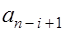 разностей между наибольшими и наименьшими значениями выборки, начиная с самых крайних
разностей между наибольшими и наименьшими значениями выборки, начиная с самых крайних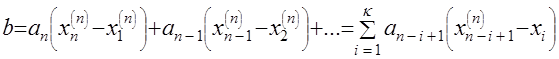 ,
, (четное), и
(четное), и  , если
, если  (нечетное).
(нечетное). , (28)
, (28) .
. и сравнить статистику
и сравнить статистику  , приведенными в виде графика на рис.1. Гипотеза о принадлежности данной выборки генеральной нормальной совокупности случайных величин принимается при
, приведенными в виде графика на рис.1. Гипотеза о принадлежности данной выборки генеральной нормальной совокупности случайных величин принимается при  и отвергается при
и отвергается при  .
.


