Самой естественной оценкой неизвестного значения дисперсии является величина 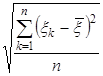 , (39)
, (39)
при которой (также на основе законов больших чисел) можно увидеть, что ее значение близко к значению дисперсии при большом 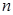 .
.
Рассмотрим задачу определения оценки неизвестного параметра  функции распределения случайной переменной
функции распределения случайной переменной  с помощью элементов пробы
с помощью элементов пробы  .
.
Некоторая функция  переменных
переменных  называется статистикой. Статистика
называется статистикой. Статистика 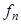 называется оценкой параметра без искажения, если выполняется соотношение
называется оценкой параметра без искажения, если выполняется соотношение  . (40)
. (40)
Прогрессия статистики  называется консистенциальной оценкой параметра
называется консистенциальной оценкой параметра  , если значение статистики
, если значение статистики  близко к значению параметра
близко к значению параметра  с большой вероятностью при больших
с большой вероятностью при больших 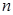 , точнее, если для каждого положительного значения
, точнее, если для каждого положительного значения 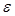 и
и  может быть найдено такое целое число
может быть найдено такое целое число  , при котором удовлетворяется неравенство
, при котором удовлетворяется неравенство
 , (41)
, (41)
если 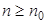 .
.
Утверждение, по которому некоторая функция рассматривается от элементов пробы  , при оценке некоторого параметра, то есть рассматривается единственное число, часто означает, что теряется некоторая информация, присутствующая в пробе
, при оценке некоторого параметра, то есть рассматривается единственное число, часто означает, что теряется некоторая информация, присутствующая в пробе  , относящаяся к параметру
, относящаяся к параметру  . В случае, когда этого не происходит, функция
. В случае, когда этого не происходит, функция  называется недостаточной статистикой. (Здесь не приводится точное математическое распределение понятия достаточной статистики).
называется недостаточной статистикой. (Здесь не приводится точное математическое распределение понятия достаточной статистики).

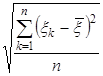 , (39)
, (39)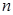 .
. функции распределения случайной переменной
функции распределения случайной переменной  с помощью элементов пробы
с помощью элементов пробы  .
. переменных
переменных 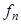 называется оценкой параметра без искажения, если выполняется соотношение
называется оценкой параметра без искажения, если выполняется соотношение  . (40)
. (40) называется консистенциальной оценкой параметра
называется консистенциальной оценкой параметра 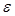 и
и  может быть найдено такое целое число
может быть найдено такое целое число  , при котором удовлетворяется неравенство
, при котором удовлетворяется неравенство , (41)
, (41)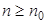 .
. называется недостаточной статистикой. (Здесь не приводится точное математическое распределение понятия достаточной статистики).
называется недостаточной статистикой. (Здесь не приводится точное математическое распределение понятия достаточной статистики).


